¶ 2016 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2016 AIME II problems here.
Discussion Forum
Engage in discussion about the 2016 AIME II math contest by visiting Random Math AIME II 2016 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2016 AIME II problems, please refer below:
Problem 1: Initially Alex, Betty, and Charlie had a total of peanuts. Charlie had the most peanuts, and Alex had the least. The three numbers of peanuts that each person had form a geometric progression. Alex eats of his peanuts, Betty eats of her peanuts, and Charlie eats of his peanuts. Now the three numbers of peanuts that each person has form an arithmetic progression. Find the number of peanuts Alex had initially.
Solution:
Problem 2: There is a chance of rain on Saturday and a chance of rain on Sunday. However, it is twice as likely to rain on Sunday if it rains on Saturday than if it does not rain on Saturday. The probability that it rains at least one day this weekend is , where and are relatively prime positive integers. Find .
Solution:
Problem 3: Let , and be real numbers satisfying the system
Find the value of .
Solution:
Problem 4: An rectangular box is built from unit cubes. Each unit cube is colored red, green, or yellow. Each of the layers of size parallel to the -faces of the box contains exactly red cubes, exactly green cubes, and some yellow cubes. Each of the layers of size parallel to the -faces of the box contains exactly green cubes, exactly yellow cubes, and some red cubes. Find the smallest possible volume of the box.
Solution:
Problem 5: Triangle has a right angle at . Its side lengths are pairwise relatively prime positive integers, and its perimeter is . Let be the foot of the altitude to , and for , let be the foot of the altitude to in . The sum . Find .
Solution:
Problem 6: For polynomial , define
Then , where and are relatively prime positive integers. Find .
Solution:
Problem 7: Squares and have a common center and . The area of is , and the area of is a smaller positive integer. Square is constructed so that each of its vertices lies on a side of and each vertex of lies on a side of . Find the difference between the largest and smallest possible integer values for the area of .
Solution:
Problem 8: Find the number of sets of three distinct positive integers with the property that the product of , and is equal to the product of , and .
Solution:
Problem 9: The sequences of positive integers and are an increasing arithmetic sequence and an increasing geometric sequence, respectively. Let . There is an integer such that and . Find .
Solution:
Problem 10: Triangle is inscribed in circle . Points and are on side with . Rays and meet again at and (other than ), respectively. If , and , then , where and are relatively prime positive integers. Find .
Solution:
Problem 11: For positive integers and , define to be -nice if there exists a positive integer such that has exactly positive divisors. Find the number of positive integers less than that are neither -nice nor -nice.
Solution:
Problem 12: The figure below shows a ring made of six small sections which you are to paint on a wall. You have four paint colors available and will paint each of the six sections a solid color. Find the number of ways you can choose to paint the sections if no two adjacent sections can be painted with the same color.
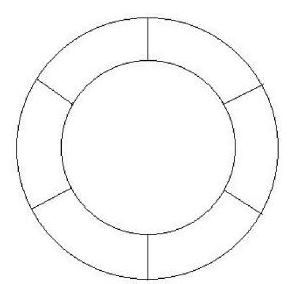
Solution:
Problem 13: Beatrix is going to place six rooks on a chessboard where both the rows and columns are labeled to ; the rooks are placed so that no two rooks are in the same row or the same column. The value of a square is the sum of its row number and column number. The score of an arrangement of rooks is the least value of any occupied square. The average score over all valid configurations is , where and are relatively prime positive integers. Find .
Solution:
Problem 14: Equilateral has side length . Points and lie outside the plane of and are on the opposite sides of the plane. Furthermore, , and , and the planes of and form a dihedral angle (the angle between the two planes). There is a point whose distance from each of , and is . Find .
Solution:
Problem 15: For let and . Let be positive real numbers such that
The maximum possible value of , where and are relatively prime positive integers. Find .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions