¶ 2007 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2007 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2007 AMC 10B math contest by visiting Random Math AMC 10B 2007 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2007 AMC 10B problems, please refer below:
Problem 1: Isabella's house has bedrooms. Each bedroom is feet long, feet wide, and feet high. Isabella must paint the walls of all the bedrooms. Doorways and windows, which will not be painted, occupy square feet in each bedroom. How many square feet of walls must be painted?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Define the operation by . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A college student drove his compact car miles home for the weekend and averaged miles per gallon. On the return trip the student drove his parents' SUV and averaged only miles per gallon. What was the average gas mileage, in miles per gallon, for the round trip?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The point is the center of the circle circumscribed about , with and , as shown. What is the degree measure of ?
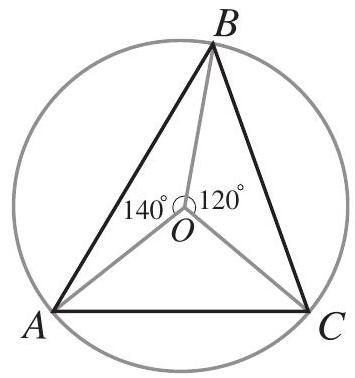
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In a certain land, all Arogs are Brafs, all Crups are Brafs, all Dramps are Arogs, and all Crups are Dramps. Which of the following statements is implied by these facts?
Answer Choices:
A. All Dramps are Brafs and are Crups.
B. All Brafs are Crups and are Dramps.
C. All Arogs are Crups and are Dramps.
D. All Crups are Arogs and are Brafs.
E. All Arogs are Dramps and some Arogs may not be Crups.
Solution:
Problem 6: The AMC will be scored by awarding points for each correct response, points for each incorrect response, and points for each problem left unanswered. After looking over the problems, Sarah has decided to attempt the first and leave only the last unanswered. How many of the first problems must she solve correctly in order to score at least points?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: All sides of the convex pentagon are of equal length, and . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: On the trip home from the meeting where this was constructed, the Contest Chair noted that his airport parking receipt had digits of the form , where , and was the average of and . How many different five-digit numbers satisfy all these properties?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A cryptographic code is designed as follows. The first time a letter appears in a given message it is replaced by the letter that is place to its right in the alphabet (assuming that the letter is one place to the right of the letter ). The second time this same letter appears in the given message, it is replaced by the letter that is places to the right, the third time it is replaced by the letter that is places to the right, and so on. For example, with this code the word "banana" becomes "cbodqg". What letter will replace the last letter in the message
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Two points and are in a plane. Let be the set of all points in the plane for which has area . Which of the following describes ?
Answer Choices:
A. two parallel lines
B. a parabola
C. a circle
D. a line segment
E. two points
Solution:
Problem 11: A circle passes through the three vertices of an isosceles triangle that has two sides of length and a base of length . What is the area of this circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Tom's age is years, which is also the sum of the ages of his three children. His age years ago was twice the sum of their ages then. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Two circles of radius are centered at and at . What is the area of the intersection of the interiors of the two circles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Some boys and girls are having a car wash to raise money for a class trip to China. Initially of the group are girls. Shortly thereafter two girls leave and two boys arrive, and then of the group are girls. How many girls were initially in the group?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The angles of quadrilateral satisfy . What is the degree measure of , rounded to the nearest whole number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A teacher gave a test to a class in which of the students are juniors and are seniors. The average score on the test was . The juniors all received the same score, and the average score of the seniors was . What score did each of the juniors receive on the test?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Point is inside equilateral . Points , and are the feet of the perpendiculars from to , and , respectively. Given that , , and , what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A circle of radius is surrounded by circles of radius as shown. What is ?
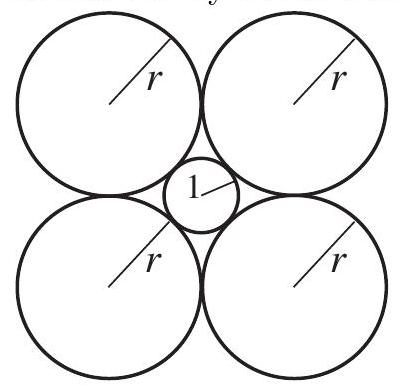
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The wheel shown is spun twice, and the randomly determined numbers opposite the pointer are recorded. The first number is divided by , and the second number is divided by . The first remainder designates a column, and the second remainder designates a row on the checkerboard shown. What is the probability that the pair of numbers designates a shaded square?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A set of square blocks is arranged into a square. How many different combinations of blocks can be selected from that set so that no two are in the same row or column?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Right has , and . Square is inscribed in with and on on , and on . What is the side length of the square?
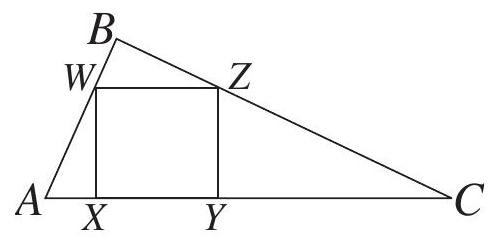
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A player chooses one of the numbers through . After the choice has been made, two regular four-sided (tetrahedral) dice are rolled, with the sides of the dice numbered through . If the number chosen appears on the bottom of exactly one die after it is rolled, then the player wins . If the number chosen appears on the bottom of both of the dice, then the player wins . If the number chosen does not appear on the bottom of either of the dice, the player loses . What is the expected return to the player, in dollars, for one roll of the dice?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A pyramid with a square base is cut by a plane that is parallel to its base and is units from the base. The surface area of the smaller pyramid that is cut from the top is half the surface area of the original pyramid. What is the altitude of the original pyramid?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let denote the smallest positive integer that is divisible by both and , and whose base- representation consists of only 's and 's, with at least one of each. What are the last four digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: How many pairs of positive integers are there such that and have no common factors greater than and
is an integer?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions