¶ 2007 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2007 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2007 AMC 10A math contest by visiting Random Math AMC 10A 2007 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2007 AMC 10A problems, please refer below:
Problem 1: One ticket to a show costs at full price. Susan buys tickets using a coupon that gives her a discount. Pam buys tickets using a coupon that gives her a discount. How many more dollars does Pam pay than Susan?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Define and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: An aquarium has a rectangular base that measures by and has a height of . It is filled with water to a height of . A brick with a rectangular base that measures by and a height of is placed in the aquarium. By how many centimeters does the water rise?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The larger of two consecutive odd integers is three times the smaller. What is their sum?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A school store sells pencils and notebooks for . It also sells pencils and notebooks for . How much do pencils and notebooks cost?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: At Euclid High School, the number of students taking the was in , in , in , in , and in , and is in . Between what two consecutive years was there the largest percentage increase?
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 7: Last year Mr. John Q. Public received an inheritance. He paid in federal taxes on the inheritance, and paid of what he had left in state taxes. He paid a total of for both taxes. How many dollars was the inheritance?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Triangles and are isosceles with and . Point is inside , and . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Real numbers and satisfy the equations and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The Dunbar family consists of a mother, a father, and some children. The average age of the members of the family is , the father is years old, and the average age of the mother and children is . How many children are in the family?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The numbers from to are placed at the vertices of a cube in such a manner that the sum of the four numbers on each face is the same. What is this common sum?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Two tour guides are leading six tourists. The guides decide to split up. Each tourist must choose one of the guides, but with the stipulation that each guide must take at least one tourist. How many different groupings of guides and tourists are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides times as fast as he walks, and both choices require the same amount of time. What is the ratio of Yan's distance from his home to his distance from the stadium?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A triangle with side lengths in the ratio is inscribed in a circle of radius . What is the area of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Four circles of radius are each tangent to two sides of a square and externally tangent to a circle of radius , as shown. What is the area of the square?
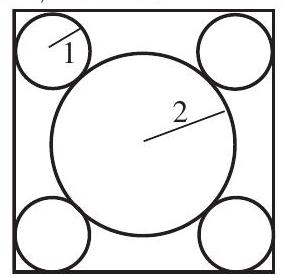
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Integers , and , not necessarily distinct, are chosen independently and at random from to , inclusive. What is the probability that is even?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Suppose that and are positive integers such that . What is the minimum possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Consider the -sided polygon , as shown. Each of its sides has length , and each two consecutive sides form a right angle. Suppose that and meet at . What is the area of quadrilateral ?
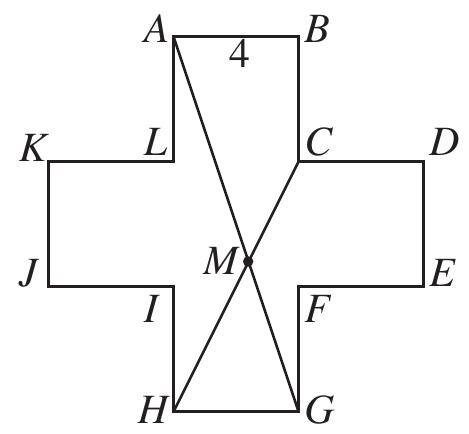
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A paint brush is swept along both diagonals of a square to produce the symmetric painted area, as shown. Half the area of the square is painted. What is the ratio of the side length of the square to the brush width?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Suppose that the number satisfies the equation . What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A sphere is inscribed in a cube that has a surface area of square meters. A second cube is then inscribed within the sphere. What is the surface area in square meters of the inner cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A finite sequence of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with terms , and and end with the term . Let be the sum of all the terms in the sequence. What is the largest prime number that always divides ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: How many ordered pairs of positive integers, with , have the property that their squares differ by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Circles centered at and each have radius , as shown. Point is the midpoint of , and . Segments and are tangent to the circles centered at and , respectively, and is a common tangent. What is the area of the shaded region ?
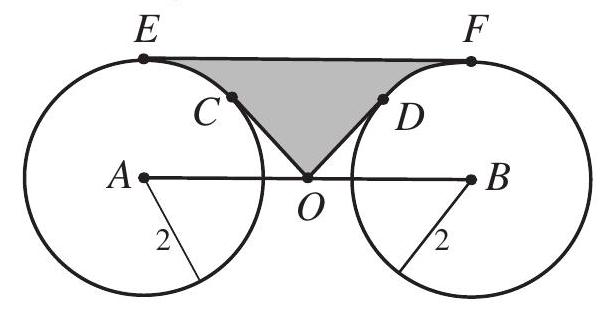
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: For each positive integer , let denote the sum of the digits of . For how many values of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions