¶ 2011 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2011 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2011 AMC 10A math contest by visiting Random Math AMC 10A 2011 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2011 AMC 10A problems, please refer below:
Problem 1: A cell phone plan costs each month, plus per text message sent, plus for each minute used over hours. In January Juan sent text messages and talked for hours. How much did he have to pay?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A small bottle of shampoo can hold milliliters of shampoo, whereas a large bottle can hold milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Suppose denotes the average of and , and denotes the average of , and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let and be the following sums of arithmetic sequences:
What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of , and minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Set has elements, and set has elements. What is the smallest possible number of elements in , the union of and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Which of the following equations does not have a solution?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Last summer of the birds living on Town Lake were geese, were swans, were herons, and were ducks. What percent of the birds that were not swans were geese?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A rectangular region is bounded by the graphs of the equations , , and , where , and are all positive numbers. Which of the following represents the area of this region?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A majority of the students in Ms. Demeanor's class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than . The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was . What was the cost of a pencil in cents?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Square has one vertex on each side of square . Point is on with . What is the ratio of the area of to the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The players on a basketball team made some three-point shots, some two-point shots, and some one-point free throws. They scored as many points with twopoint shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team's total score was points. How many free throws did they make?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many even integers are there between and whose digits are all different and come from the set ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A pair of standard -sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle's circumference?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of gallons per mile. On the whole trip he averaged miles per gallon. How long was the trip in miles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Which of the following is equal to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In the eight-term sequence , the value of is and the sum of any three consecutive terms is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Circles , and each have radius . Circles and share one point of tangency. Circle has a point of tangency with the midpoint of . What is the area inside circle but outside circle and circle ?
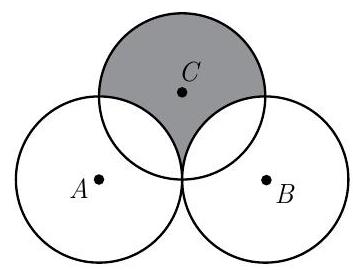
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In the population of a town was a perfect square. Ten years later, after an increase of people, the population was more than a perfect square. Now, in , with an increase of another people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town's population during this twenty-year period?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Two points on the circumference of a circle of radius are selected independently and at random. From each point a chord of length is drawn in a clockwise direction. What is the probability that the two chords intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two counterfeit coins of equal weight are mixed with identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the coins. A second pair is selected at random without replacement from the remaining coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all selected coins are genuine?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Each vertex of convex pentagon is to be assigned a color. There are colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Seven students count from to as follows:
. Alice says all of the numbers, except she skips the middle number in each consecutive group of three numbers. That is, Alice says .
. Barbara says all of the numbers that Alice doesn't say, except she also skips the middle number in each consecutive group of three numbers.
. Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers.
. Debbie, Eliza, and Fatima say all of the numbers that none of the students with first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.
. Finally, George says the only number that no one else says.
What number does George say?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a square region and an integer. A point in the interior of is called -ray partitional if there are rays emanating from that divide into triangles of equal area. How many points are -ray partitional but not -ray partitional?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions