¶ 2011 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2011 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2011 AMC 10B math contest by visiting Random Math AMC 10B 2011 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2011 AMC 10B problems, please refer below:
Problem 1: What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Josanna's test scores to date are , and . Her goal is to raise her test average at least points with her next test. What is the minimum test score she would need to accomplish this goal?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: At a store, when a length is reported as inches that means the length is at least inches and at most inches. Suppose the dimensions of a rectangular tile are reported as inches by inches. In square inches, what is the minimum area for the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: LeRoy and Bernardo went on a week-long trip together and agreed to share the costs equally. Over the week, each of them paid for various joint expenses such as gasoline and car rental. At the end of the trip it turned out that LeRoy had paid dollars and Bernardo had paid dollars, where . How many dollars must LeRoy give to Bernardo so that they share the costs equally?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In multiplying two positive integers and , Ron reversed the digits of the two-digit number . His erroneous product was . What is the correct value of the product of and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: On Halloween Casper ate of his candies and then gave candies to his brother. The next day he ate of his remaining candies and then gave candies to his sister. On the third day he ate his final candies. How many candies did Casper have at the beginning?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The sum of two angles of a triangle is of a right angle, and one of these two angles is larger than the other. What is the degree measure of the largest angle in the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: At a certain beach if it is at least and sunny, then the beach will be crowded. On June the beach was not crowded. What can be concluded about the weather conditions on June ?
Answer Choices:
A. The temperature was cooler than and it was not sunny.
B. The temperature was cooler than or it was not sunny.
C. If the temperature was at least , then it was sunny.
D. If the temperature was cooler than , then it was sunny.
E. If the temperature was cooler than , then it was not sunny.
Solution:
Problem 9: The area of is one third of the area of . Segment is perpendicular to segment . What is ?
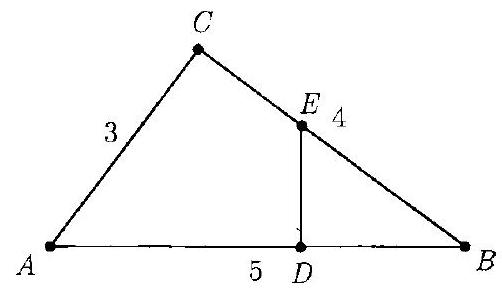
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Consider the set of numbers . The ratio of the largest element of the set to the sum of the other ten elements of the set is closest to which integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: There are people in a room. What is the largest value of such that the statement "At least people in this room have birthdays falling in the same month." is always true?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Keiko walks once around a track at exactly the same constant speed every day. The sides of the track are straight, and the ends are semicircles. The track has width meters, and it takes her seconds longer to walk around the outside edge of the track than around the inside edge. What is Keiko's speed in meters per second?
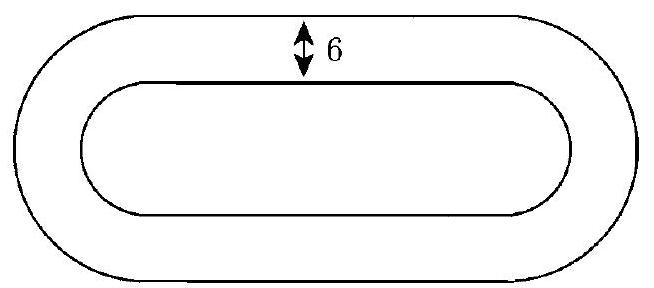
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Two real numbers are selected independently at random from the interval . What is the probability that the product of those numbers is greater than zero?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A rectangular parking lot has a diagonal of meters and an area of square meters. In meters, what is the perimeter of the parking lot?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let @ denote the "averaged with" operation: . Which of the following distributive laws hold for all numbers , and ?
Answer Choices:
A. only
B. only
C. only
D. and only
E. and only
Solution:
Problem 16: A dart board is a regular octagon divided into regions as shown. Suppose that a dart thrown at the board is equally likely to land anywhere on the board. What is the probability that the dart lands within the center square?
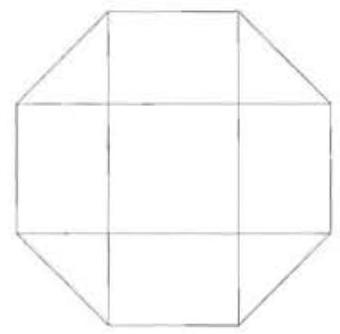
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In the given circle, the diameter is parallel to , and is parallel to . The angles and are in the ratio . What is the degree measure of angle ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Rectangle has and . Point is chosen on side so that . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: What is the product of all the roots of the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Rhombus has side length and . Region consists of all points inside the rhombus that are closer to vertex than any of the other three vertices. What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Brian writes down four integers whose sum is . The pairwise positive differences of these numbers are , and . What is the sum of the possible values for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A pyramid has a square base with sides of length and has lateral faces that are equilateral triangles. A cube is placed within the pyramid so that one face is on the base of the pyramid and its opposite face has all its edges on the lateral faces of the pyramid. What is the volume of this cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: What is the hundreds digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A lattice point in an -coordinate system is any point where both and are integers. The graph of passes through no lattice point with for all such that . What is the maximum possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a triangle with sides , and . For , if and , and are the points of tangency of the incircle of to the sides , and , respectively, then is a triangle with side lengths , and , if it exists. What is the perimeter of the last triangle in the sequence ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions