¶ 2012 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2012 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2012 AMC 10A math contest by visiting Random Math AMC 10A 2012 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2012 AMC 10A problems, please refer below:
Problem 1: Cagney can frost a cupcake every seconds and Lacey can frost a cupcake every seconds. Working together, how many cupcakes can they frost in minutes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A square with side length is cut in half, creating two congruent rectangles. What are the dimensions of one of these rectangles?
Answer Choices:
A. by
B. by
C. by
D. by
E. by
Solution:
Problem 3: A bug crawls along a number line, starting at . It crawls to , then turns around and crawls to . How many units does the bug crawl altogether?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let and . What is the smallest possible degree measure for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Last year adult cats, half of whom were female, were brought into the Smallville Animal Shelter. Half of the adult female cats were accompanied by a litter of kittens. The average number of kittens per litter was . What was the total number of cats and kittens received by the shelter last year?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The product of two positive numbers is . The reciprocal of one of these numbers is times the reciprocal of the other number. What is the sum of the two numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: In a bag of marbles, of the marbles are blue and the rest are red. If the number of red marbles is doubled and the number of blue marbles stays the same, what fraction of the marbles will be red?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The sums of three whole numbers taken in pairs are , and . What is the middle number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A pair of six-sided fair dice are labeled so that one die has only even numbers (two each of , and ), and the other die has only odd numbers (two each of , and ). The pair of dice is rolled. What is the probability that the sum of the numbers on the tops of the two dice is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Mary divides a circle into sectors. The central angles of these sectors, measured in degrees, are all integers and they form an arithmetic sequence. What is the degree measure of the smallest possible sector angle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Externally tangent circles with centers at points and have radii of lengths and , respectively. A line externally tangent to both circles intersects ray at point . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A year is a leap year if and only if the year number is divisible by (such as ) or is divisible by but not by (such as ). The th anniversary of the birth of novelist Charles Dickens was celebrated on February , a Tuesday. On what day of the week was Dickens born?
Answer Choices:
A. Friday
B. Saturday
C. Sunday
D. Monday
E. Tuesday
Solution:
Problem 13: An iterative average of the numbers , and is computed in the following way. Arrange the five numbers in some order. Find the mean of the first two numbers, then find the mean of that with the third number, then the mean of that with the fourth number, and finally the mean of that with the fifth number. What is the difference between the largest and smallest possible values that can be obtained using this procedure?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Chubby makes nonstandard checkerboards that have squares on each side. The checkerboards have a black square in every corner and alternate red and black squares along every row and column. How many black squares are there on such a checkerboard?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Three unit squares and two line segments connecting two pairs of vertices are shown. What is the area of ?
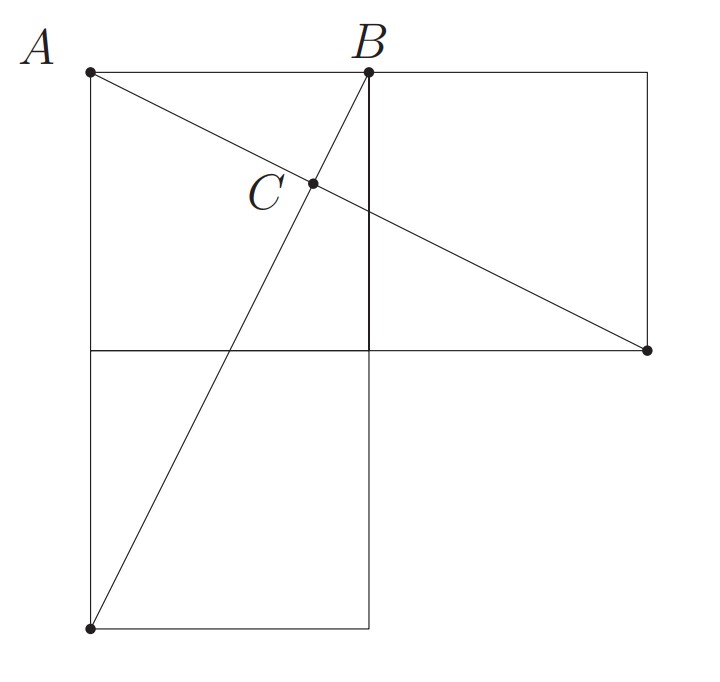
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Three runners start running simultaneously from the same point on a -meter circular track. They each run clockwise around the course maintaining constant speeds of , and meters per second. The runners stop once they are all together again somewhere on the circular course. How many seconds do the runners run?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let and be relatively prime integers with and
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The closed curve in the figure is made up of congruent circular arcs each of length , where each of the centers of the corresponding circles is among the vertices of a regular hexagon of side . What is the area enclosed by the curve?
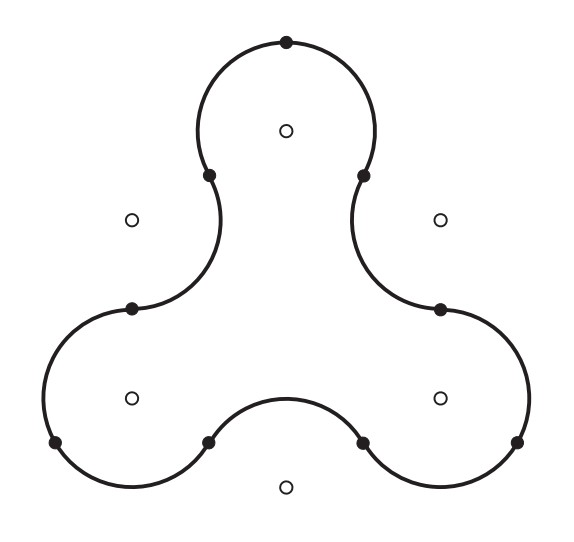
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Paula the painter and her two helpers each paint at constant, but different, rates. They always start at AM, and all three always take the same amount of time to eat lunch. On Monday the three of them painted of a house, quitting at PM. On Tuesday, when Paula wasn't there, the two helpers painted only of the house and quit at PM. On Wednesday Paula worked by herself and finished the house by working until PM. How long, in minutes, was each day's lunch break?
Answer Choices:
A. 30
B.
C.
D.
E.
Solution:
Problem 20: A square is partitioned into unit squares. Each unit square is painted either white or black with each color being equally likely, chosen independently and at random. The square is then rotated clockwise about its center, and every white square in a position formerly occupied by a black square is painted black. The colors of all other squares are left unchanged. What is the probability that the grid is now entirely black?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let points , and . Points , , and are midpoints of line segments , and respectively. What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The sum of the first positive odd integers is more than the sum of the first positive even integers. What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Adam, Benin, Chiang, Deshawn, Esther, and Fiona have internet accounts. Some, but not all, of them are internet friends with each other, and none of them has an internet friend outside this group. Each of them has the same number of internet friends. In how many different ways can this happen?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let , and be positive integers with such that
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Real numbers , and are chosen independently and at random from the interval for some positive integer . The probability that no two of , and are within unit of each other is greater than . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions