¶ 2012 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2012 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2012 AMC 10B math contest by visiting Random Math AMC 10B 2012 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2012 AMC 10B problems, please refer below:
Problem 1: Each third-grade classroom at Pearl Creek Elementary has students and pet rabbits. How many more students than rabbits are there in all of the third-grade classrooms?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A circle of radius is inscribed in a rectangle as shown. The ratio of the length of the rectangle to its width is . What is the area of the rectangle?
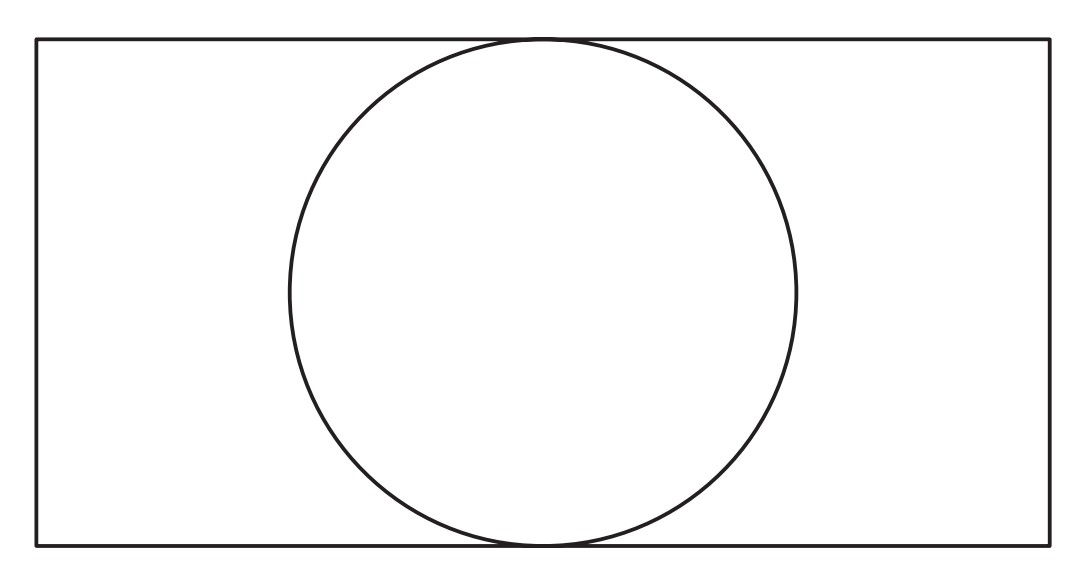
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The point in the -plane with coordinates is reflected across the line . What are the coordinates of the reflected point?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: When Ringo places his marbles into bags with marbles per bag, he has marbles left over. When Paul does the same with his marbles, he has marbles left over. Ringo and Paul pool their marbles and place them into as many bags as possible, with marbles per bag. How many marbles will be left over?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Anna enjoys dinner at a restaurant in Washington, D.C., where the sales tax on meals is . She leaves a tip on the price of her meal before the sales tax is added, and the tax is calculated on the pre-tip amount. She spends a total of for dinner. What is the cost of her dinner without tax or tip?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In order to estimate the value of where and are real numbers with , Xiaoli rounded up by a small amount, rounded down by the same amount, and then subtracted her rounded values. Which of the following statements is necessarily correct?
Answer Choices:
A. Her estimate is larger than .
B. Her estimate is smaller than .
C. Her estimate equals .
D. Her estimate equals .
E. Her estimate is .
Solution:
Problem 7: For a science project, Sammy observed a chipmunk and a squirrel stashing acorns in holes. The chipmunk hid acorns in each of the holes it dug. The squirrel hid acorns in each of the holes it dug. They each hid the same number of acorns, although the squirrel needed fewer holes. How many acorns did the chipmunk hide?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: What is the sum of all integer solutions to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Two integers have a sum of . When two more integers are added to the first two integers the sum is . Finally when two more integers are added to the sum of the previous four integers the sum is . What is the minimum number of even integers among the integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: How many ordered pairs of positive integers satisfy the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A dessert chef prepares the dessert for every day of a week starting with Sunday. The dessert each day is either cake, pie, ice cream, or pudding. The same dessert may not be served two days in a row. There must be cake on Friday because of a birthday. How many different dessert menus for the week are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Point is due east of point . Point is due north of point . The distance between points and is meters, and . Point is meters due north of point . The distance is between which two integers?
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 13: It takes Clea seconds to walk down an escalator when it is not operating, and only seconds to walk down the escalator when it is operating. How many seconds does it take Clea to ride down the operating escalator when she just stands on it?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Two equilateral triangles are contained in a square whose side length is . The bases of these triangles are the opposite sides of the square, and their intersection is a rhombus. What is the area of the rhombus?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: In a round-robin tournament with teams, each team plays one game against each other team, and each game results in one team winning and one team losing. At the end of the tournament, the teams are ranked by the number of games won. What is the maximum number of teams that could be tied for the most wins at the end of the tournament?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Three circles with radius are mutually tangent. What is the total area of the circles and the region bounded by them, as shown in the figure?
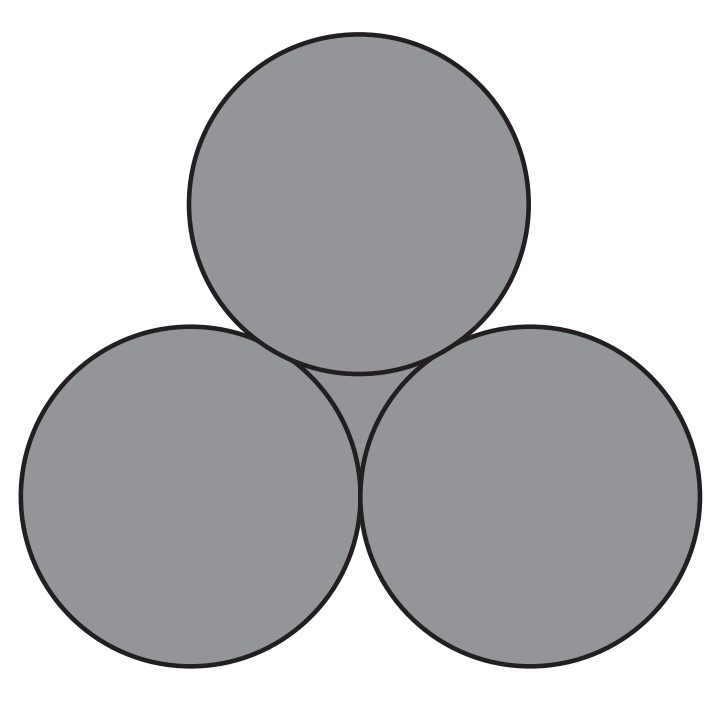
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Jesse cuts a circular paper disk of radius along two radii to form two sectors, the smaller having a central angle of degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Suppose that one of every people in a certain population has a particular disease, which displays no symptoms. A blood test is available for screening for this disease. For a person who has this disease, the test always turns out positive. For a person who does not have the disease, however, there is a false positive rate - in other words, for such people, of the time the test will turn out negative, but of the time the test will turn out positive and will incorrectly indicate that the person has the disease. Let be the probability that a person who is chosen at random from this population and gets a positive test result actually has the disease. Which of the following is closest to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In rectangle , and is the midpoint of . Segment is extended units beyond to point , and is the intersection of and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Bernardo and Silvia play the following game. An integer between and , inclusive, is selected and given to Bernardo. Whenever Bernardo receives a number, he doubles it and passes the result to Silvia. Whenever Silvia receives a number, she adds to it and passes the result to Bernardo. The winner is the last person who produces a number less than . Let be the smallest initial number that results in a win for Bernardo. What is the sum of the digits of ?
Answer Choices:
A. 7
B.
C.
D.
E.
Solution:
Problem 21: Four distinct points are arranged in a plane so that the segments connecting them have lengths , and . What is the ratio of to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be a list of the first positive integers such that for each either or or both appear somewhere before in the list. How many such lists are there?
Answer Choices:
A. 120
B.
C.
D.
E.
Solution:
Problem 23: A solid tetrahedron is sliced off a solid wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Amy, Beth, and Jo listen to four different songs and discuss which ones they like. No song is liked by all three. Furthermore, for each of the three pairs of the girls, there is at least one song liked by those two girls but disliked by the third. In how many different ways is this possible?
Answer Choices:
A. 108
B.
C.
D.
E.
Solution:
Problem 25: A bug travels from to along the segments in the hexagonal lattice pictured below. The segments marked with an arrow can be traveled only in the direction of the arrow, and the bug never travels the same segment more than once. How many different paths are there?
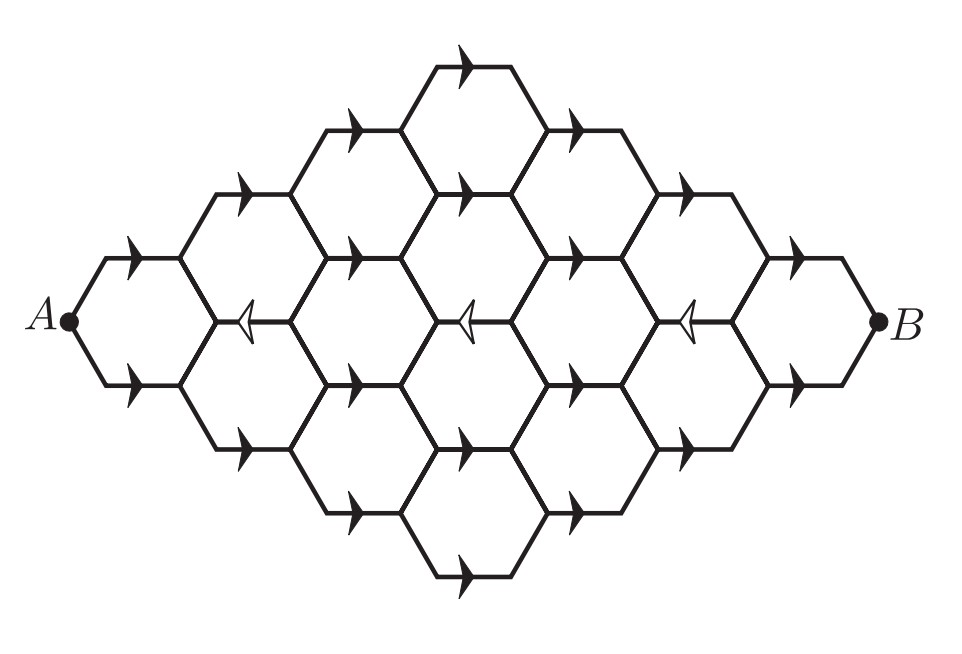
Answer Choices:
A. 2112
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions