¶ 2017 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2017 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2017 AMC 10B math contest by visiting Random Math AMC 10B 2017 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2017 AMC 10B problems, please refer below:
Problem 1: Mary thought of a positive two-digit number. She multiplied it by and added . Then she switched the digits of the result, obtaining a number between and , inclusive. What was Mary's number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Sofia ran laps around the -meter track at her school. For each lap, she ran the first meters at an average speed of meters per second and the remaining meters at an average speed of meters per second. How much time did Sofia take running the laps?
Answer Choices:
A. minutes and seconds
B. minutes and seconds
C. minutes and seconds
D. minutes and seconds
E. minutes and seconds
Solution:
Problem 3: Real numbers , and satisfy the inequalities
Which of the following numbers is necessarily positive?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Suppose that and are nonzero real numbers such that
What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Camilla had twice as many blueberry jelly beans as cherry jelly beans. After eating pieces of each kind, she now has three times as many blueberry jelly beans as cherry jelly beans. How many blueberry jelly beans did she originally have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: What is the largest number of solid -in -in -in blocks that can fit in a -in -in -in box?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Samia set off on her bicycle to visit her friend, traveling at an average speed of kilometers per hour. When she had gone half the distance to her friend's house, a tire went flat, and she walked the rest of the way at kilometers per hour. In all it took her minutes to reach her friend's house. In kilometers rounded to the nearest tenth, how far did Samia walk?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Points and are vertices of with . The altitude from meets the opposite side at . What are the coordinates of point ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A radio program has a quiz consisting of multiple-choice questions, each with choices. A contestant wins if he or she gets or more of the questions right. The contestant answers randomly to each question. What is the probability of winning?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The lines with equations and are perpendicular and intersect at . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: At Typico High School, of the students like dancing, and the rest dislike it. Of those who like dancing, say that they like it, and the rest say that they dislike it. Of those who dislike dancing, say that they dislike it, and the rest say that they like it. What fraction of students who say they dislike dancing actually like it?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Elmer's new car gets better fuel efficiency, measured in kilometers per liter, than his old car. However, his new car uses diesel fuel, which is more expensive per liter than the gasoline his old car uses. By what percent will Elmer save money if he uses his new car instead of his old car for a long trip?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: There are students participating in an after-school program offering classes in yoga, bridge, and painting. Each student must take at least one of these three classes, but may take two or all three. There are students taking yoga, taking bridge, and taking painting. There are students taking at least two classes. How many students are taking all three classes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: An integer is selected at random in the range . What is the probability that the remainder when is divided by is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Rectangle has and . Point is the foot of the perpendicular from to diagonal . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: How many of the base-ten numerals for the positive integers less than or equal to contain the digit ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Call a positive integer monotonous if it is a one-digit number or its digits, when read from left to right, form either a strictly increasing or a strictly decreasing sequence. For example, , and are monotonous, but , and are not. How many monotonous positive integers are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: In the figure below, of the disks are to be painted blue, are to be painted red, and is to be painted green. Two paintings that can be obtained from one another by a rotation or a reflection of the entire figure are considered the same. How many different paintings are possible?
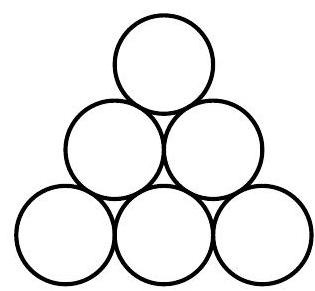
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Let be an equilateral triangle. Extend side beyond to a point so that . Similarly, extend side beyond to a point so that , and extend side beyond to a point so that . What is the ratio of the area of to the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The number has over positive integer divisors. One of them is chosen at random. What is the probability that it is odd?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: In , and is the midpoint of . What is the sum of the radii of the circles inscribed in and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The diameter of a circle of radius is extended to a point outside the circle so that . Point is chosen so that and line is perpendicular to line . Segment intersects the circle at a point between and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Let be the -digit number that is formed by writing the integers from to in order, one after the other. What is the remainder when is divided by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The vertices of an equilateral triangle lie on the hyperbola , and a vertex of this hyperbola is the centroid of the triangle. What is the square of the area of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Last year Isabella took math tests and received different scores, each an integer between and , inclusive. After each test she noticed that the average of her test scores was an integer. Her score on the seventh test was . What was her score on the sixth test?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions