¶ 2022 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2022 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2022 AMC 10B math contest by visiting Random Math AMC 10B 2022 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2022 AMC 10B problems, please refer below:
Problem 1: Define to be for all real numbers and . What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: In rhombus , point lies on segment such that , and . What is the area of ?
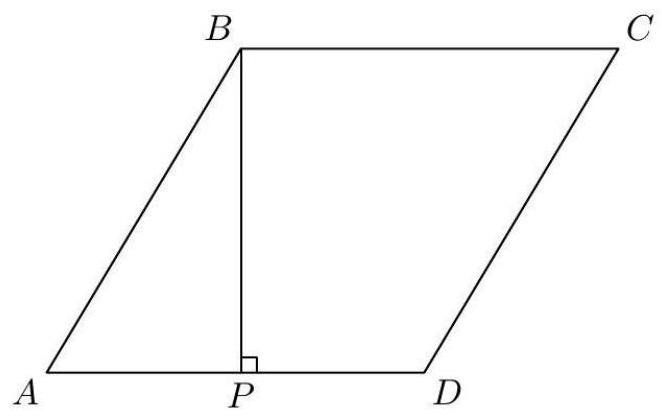
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: How many three-digit positive integers have an odd number of even digits?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A donkey suffers an attack of hiccups and the first hiccup happens at one afternoon. Suppose that the donkey hiccups regularly every seconds. At what time does the donkey's th hiccup occur?
Answer Choices:
A. seconds after
B. seconds after
C. seconds after
D. seconds after
E. seconds after
Solution:
Problem 5: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: How many of the first ten numbers of the sequence are prime numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: For how many values of the constant will the polynomial have two distinct integer roots?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Consider the following sets of elements each:
How many of these sets contain exactly two multiples of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The sum
can be expressed as , where and are positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Camila writes down five positive integers. The unique mode of these integers is greater than their median, and the median is greater than their arithmetic mean. What is the least possible value for the mode?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: All the high schools in a large school district are involved in a fundraiser selling T-shirts. Which of the choices below is logically equivalent to the statement "No school bigger than Euclid HS sold more T-shirts than Euclid HS"?
Answer Choices:
A. All schools smaller than Euclid HS sold fewer T-shirts than Euclid HS.
B. No school that sold more T-shirts than Euclid HS is bigger than Euclid HS.
C. All schools bigger than Euclid HS sold fewer T-shirts than Euclid HS.
D. All schools that sold fewer T-shirts than Euclid HS are smaller than Euclid HS.
E. All schools smaller than Euclid HS sold more T-shirts than Euclid HS.
Solution:
Problem 12: A pair of fair -sided dice is rolled times. What is the least value of such that the probability that the sum of the numbers face up on a roll equals at least once is greater than ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The positive difference between a pair of primes is equal to , and the positive difference between the cubes of the two primes is . What is the sum of the digits of the least prime that is greater than those two primes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Suppose that is a subset of such that the sum of any two (not necessarily distinct) elements of is never an element of . What is the maximum number of elements may contain?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let be the sum of the first term of an arithmetic sequence that has a common difference of . The quotient does not depend on . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The diagram below shows a rectangle with side lengths and and a square with side length . Three vertices of the square lie on three different sides of the rectangle, as shown. What is the area of the region inside both the square and the rectangle?
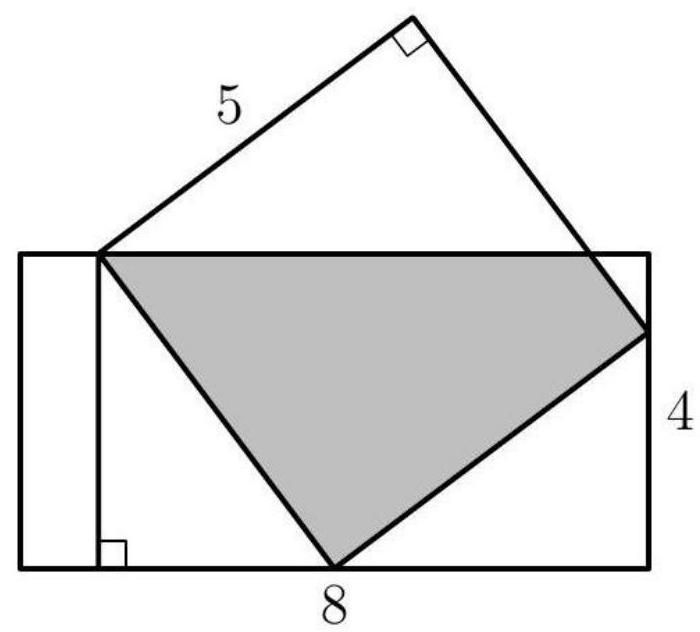
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: One of the following numbers is not divisible by any prime number less than . Which is it?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Consider systems of three linear equations with unknowns , and ,
where each of the coefficients is either or and the system has a solution other than . For example, one such system is
with a nonzero solution of . How many such systems are there? (The equations in a system need not be distinct, and two systems containing the same equations in a different order are considered different.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Each square in a grid is either filled or empty, and has up to eight adjacent neighboring squares, where neighboring squares share either a side or a corner. The grid is transformed by the following rules:
Any filled square with two or three filled neighbors remains filled. Any empty square with exactly three filled neighbors becomes a filled square. All other squares remain empty or become empty. A sample transformation is shown in the figure below.
.jpg)
.jpg)
Initial Transformed
Suppose the grid has a border of empty squares surrounding a subgrid. How many initial configurations will lead to a transformed grid consisting of a single filled square in the center after a single transformation? (Rotations and reflections of the same configuration are considered different.)
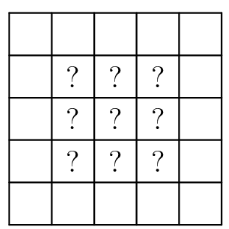
.jpg)
Initial Transformed
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let be a rhombus with . Let be the midpoint of , and let be the point on such that is perpendicular to . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let be a polynomial with rational coefficients such that when is divided by the polynomial , the remainder is , and when is divided by the polynomial , the remainder is . There is a unique polynomial of least degree with these two properties. What is the sum of the squares of the coefficients of that polynomial?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be the set of circles in the coordinate plane that are tangent to each of the three circles with equations , and . What is the sum of the areas of all circles in ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Ant Amelia starts on the number line at and crawls in the following manner. For , Amelia chooses a time duration and an increment independently and uniformly at random from the interval . During the th step of the process, Amelia moves units in the positive direction, using up minutes. If the total elapsed time has exceeded minute during the th step, she stops at the end of that step; otherwise, she continues with the next step, taking at most steps in all. What is the probability that Amelia's position when she stops will be greater than ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Consider functions that satisfy
for all real numbers and . Of all such functions that also satisfy the equation , what is the greatest possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a sequence of numbers, where each is either or . For each positive integer , define
Suppose for all . What is the value of the sum
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions