¶ 2023 AMC10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2023 AMC10A problems here.
Discussion Forum
Engage in discussion about the 2023 AMC10A math contest by visiting Random Math AMC10A 2023 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2023 AMC10A problems, please refer below:
Problem 1: Cities and are miles apart. Alicia lives in and Beth lives in . Alicia bikes towards at miles per hour. Leaving at the same time, Beth bikes toward at miles per hour. How many miles from City will they be when they meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The weight of of a large pizza together with cups of orange slices is the same as the weight of of a large pizza together with cup of orange slices. A cup of orange slices weighs of a pound. What is the weight, in pounds, of a large pizza?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: How many positive perfect squares less than are divisible by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A quadrilateral has all integer side lengths, a perimeter of , and one side of length . What is the greatest possible length of one side of this quadrilateral?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: How many digits are in the base-ten representation of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: An integer is assigned to each vertex of a cube. The value of an edge is defined to be the sum of the values of the two vertices it touches, and the value of a face is defined to be the sum of the values of the four edges surrounding it. The value of the cube is defined as the sum of the values of its six faces. Suppose the sum of the integers assigned to the vertices is . What is the value of the cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Janet rolls a standard -sided die times and keeps a running total of the numbers she rolls. What is the probability that at some point, her running total will equal ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Barb the baker has developed a new temperature scale for her bakery called the Breadus scale, which is a linear function of the Fahrenheit scale. Bread rises at degrees Fahrenheit, which is degrees on the Breadus scale. Bread is baked at degrees Fahrenheit, which is degrees on the Breadus scale. Bread is done when its internal temperature is degrees Fahrenheit. What is this in degrees on the Breadus scale?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A digital display shows the current date as an -digit integer consisting of a -digit year, followed by a -digit month, followed by a -digit date within the month. For example, Arbor Day this year is displayed as . For how many dates in does each digit appear an even number of times in the -digit display for that date?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Maureen is keeping track of the mean of her quiz scores this semester. If Maureen scores an on the next quiz, her mean will increase by . If she scores an on each of the next three quizzes, her mean will increase by . What is the mean of her quiz scores currently?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
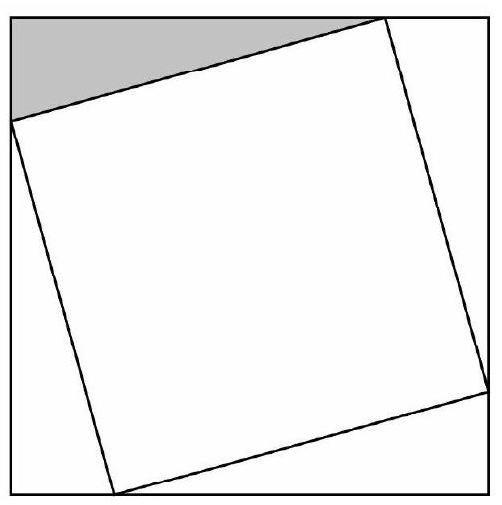
Problem 11: A square of area is inscribed in a square of area , creating four congruent triangles, as shown below. What is the ratio of the shorter leg to the longer leg in the shaded right triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: How many three-digit positive integers satisfy the following properties?
-
The number is divisible by .
-
The number formed by reversing the digits of is divisible by .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Abdul and Chiang are standing feet apart in a field. Bharat is standing in the same field as far from Abdul as possible so that the angle formed by his lines of sight to Abdul and Chiang measures . What is the square of the distance (in feet) between Abdul and Bharat?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A number is chosen at random from among the first positive integers, and a positive integer divisor of that number is then chosen at random. What is the probability that the chosen divisor is divisible by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: An even number of circles are nested, starting with a radius of and increasing by each time, all sharing a common point. The region between every other circle is shaded, starting with the region inside the circle of radius but outside the circle of radius . An example showing circles is displayed below. What is the least number of circles needed to make the total shaded area at least ?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In a table tennis tournament every participant played every other participant exactly once. Although there were twice as many right-handed players as left-handed players, the number of games won by left-handed players was more than the number of games won by right-handed players (there were no ties and no ambidextrous players). What is the total number of games played?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let be a rectangle with and . Points and lie on and , respectively, so that all sides of , and have integer lengths. What is the perimeter of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A rhombic dodecahedron is a convex polyhedron where each of the faces is a rhombus, and all of the faces are congruent to each other. The number of edges that meet at a vertex is either , depending on the vertex. What is the number of vertices at which exactly edges meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The line segment from to can be transformed to the line segment from to , sending to and to , by a rotation centered at the point . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
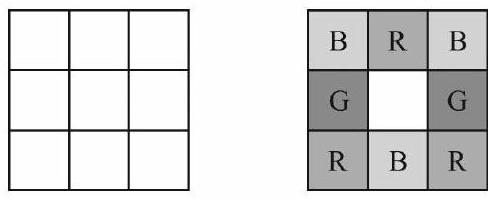
Problem 20: Each square in a grid of squares is colored red, white, blue, or green so that every square contains one square of each color. One such coloring is shown on the right below. How many different colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let be the unique polynomial of minimal degree with the following properties:
- has leading coefficient ,
- is a root of ,
- is a root of ,
- is a root of , and
- is a root of .
The roots of are integers, with one exception. The root that is not an integer can be written as , where and are relatively prime positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
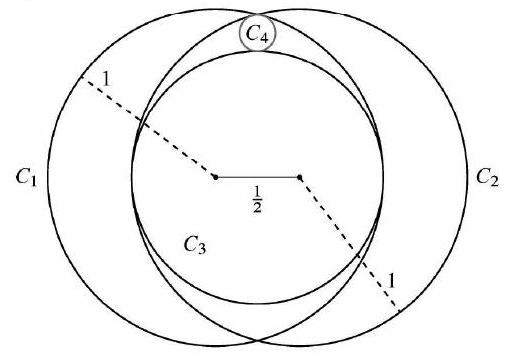
Problem 22: Circles and each have radius , and the distance between their centers is . Circle is the largest circle internally tangent to both and . Circle is internally tangent to both and and externally tangent to . What is the radius of C_
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If the positive integer has positive integer divisors and with , then and are said to be complementary divisors of . Suppose that is a positive integer that has one complementary pair of divisors that differ by and another pair of complementary divisors that differ by . What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
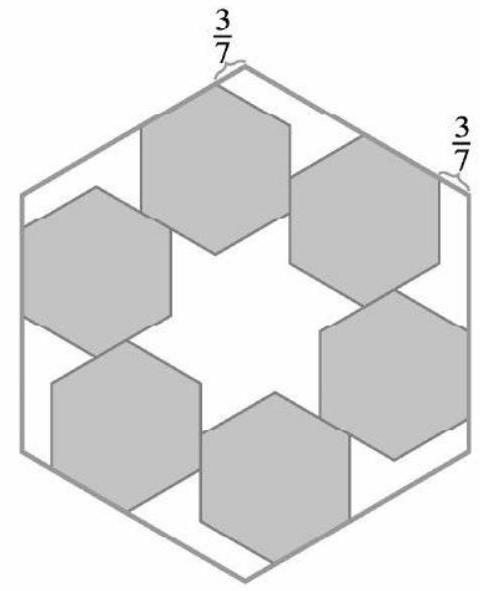
Problem 24: Six regular hexagonal blocks of side length unit are arranged inside a regular hexagonal frame. Each block lies along an inside edge of the frame and is aligned with two other blocks, as shown in the figure below. The distance from any corner of the frame to the nearest vertex of a block is unit. What is the area of the region inside the frame not occupied by the blocks?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: If and are vertices of a polyhedron, define the distance to be the minimum number of edges of the polyhedron one must traverse in order to connect and . For example, if is an edge of the polyhedron, then , but if and are edges and is not an edge, then . Let , and be randomly chosen distinct vertices of a regular icosahedron (regular polyhedron made up of equilateral triangles). What is the probability that ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions