¶ 2003 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2003 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2003 AMC 12B math contest by visiting Random Math AMC 12B 2003 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2003 AMC 12B problems, please refer below:
Problem 1: Which of the following is the same as
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al's pills cost a total of for the two weeks. How much does one green pill cost?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the figure. She plants one flower per square foot in each region. Asters cost each, begonias each, cannas each, dahlias each, and Easter lilies each. What is the least possible cost, in dollars, for her garden?
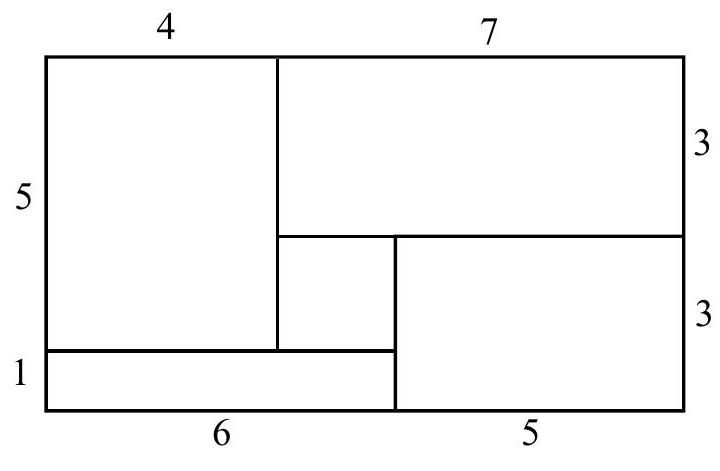
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a " -inch" television screen is closest, in inches, to which of the following?
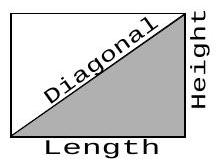
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Penniless Pete's piggy bank has no pennies in it, but it has coins, all nickels, dimes, and quarters, whose total value is . It does not necessarily contain coins of all three types. What is the difference between the largest and smallest number of dimes that could be in the bank?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Let be a linear function for which . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Several figures can be made by attaching two equilateral triangles to the regular pentagon in two of the five positions shown. How many non-congruent figures can be constructed in this way?
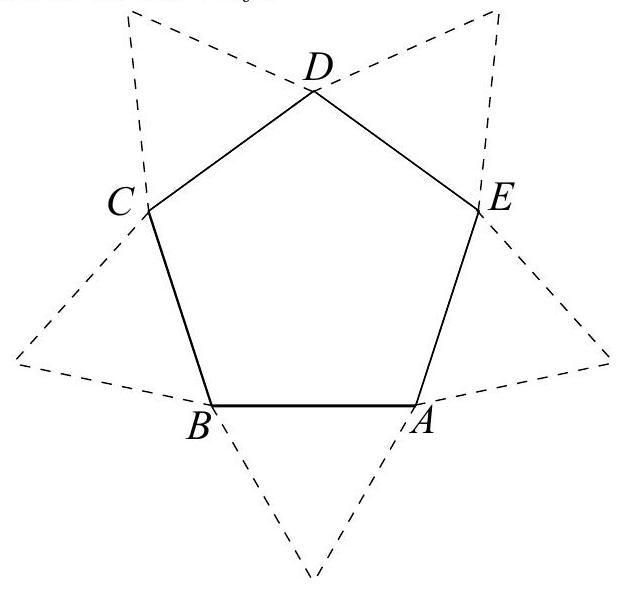
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Cassandra sets her watch to the correct time at noon. At the actual time of PM, she notices that her watch reads and seconds. Assuming that her watch loses time at a constant rate, what will be the actual time when her watch first reads PM?
Answer Choices:
A. PM and seconds
B. PM
C. PM
D. PM
E. PM
Solution:
Problem 12: What is the largest integer that is a divisor of
for all positive even integers ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone's height to its radius?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: In rectangle and . Points and are on so that and . Lines and intersect at . Find the area of .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A regular octagon has an area of one square unit. What is the area of the rectangle ?
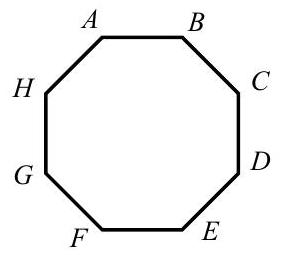
Answer Choices:
A.
B.
C.
D.
E.
Solution:
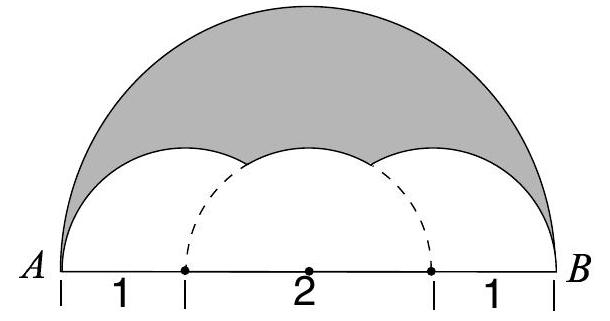
Problem 16: Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If and , what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let and be positive integers such that . The minimum possible value of has a prime factorization . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Let be the set of permutations of the sequence for which the first term is not . A permutation is chosen randomly from . The probability that the second term is , in lowest terms, is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Part of the graph of is shown. What is ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: An object moves in a straight line from to , turns at an angle , measured in radians and chosen at random from the interval , and moves in a straight line to . What is the probability that ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
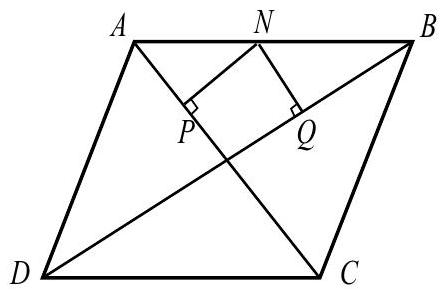
Problem 22: Let be a rhombus with and . Let be a point on , and let and be the feet of the perpendiculars from to and , respectively. Which of the following is closest to the minimum possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The number of -intercepts on the graph of in the interval is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Positive integers , and are chosen so that , and the system of equations
has exactly one solution. What is the minimum value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Three points are chosen randomly and independently on a circle. What is the probability that all three pairwise distances between the points are less than the radius of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions