¶ 2004 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2004 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2004 AMC 12B math contest by visiting Random Math AMC 12B 2004 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2004 AMC 12B problems, please refer below:
Problem 1: At each basketball practice last week, Jenny made twice as many free throws as she made at the previous practice. At her fifth practice she made free throws. How many free throws did she make at the first practice?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: In the expression , the values of , and are , and , although not necessarily in that order. What is the maximum possible value of the result?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If and are positive integers for which , what is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: An integer , with , is to be chosen. If all choices are equally likely, what is the probability that at least one digit of is a ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: On a trip from the United States to Canada, Isabella took U.S. dollars. At the border she exchanged them all, receiving Canadian dollars for every U.S. dollars. After spending Canadian dollars, she had Canadian dollars left. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Minneapolis-St. Paul International Airport is miles southwest of downtown St. Paul and miles southeast of downtown Minneapolis. Which of the following is closest to the number of miles between downtown St. Paul and downtown Minneapolis?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: A square has sides of length , and a circle centered at one of its vertices has radius . What is the area of the union of the regions enclosed by the square and the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A grocer makes a display of cans in which the top row has one can and each lower row has two more cans than the row above it. If the display contains cans, how many rows does it contain?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The point is rotated clockwise around the origin to point . Point is then reflected in the line to point . What are the coordinates of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: An annulus is the region between two concentric circles. The concentric circles in the figure have radii and , with . Let be a radius of the larger circle, let be tangent to the smaller circle at , and let be the radius of the larger circle that contains . Let , and . What is the area of the annulus?
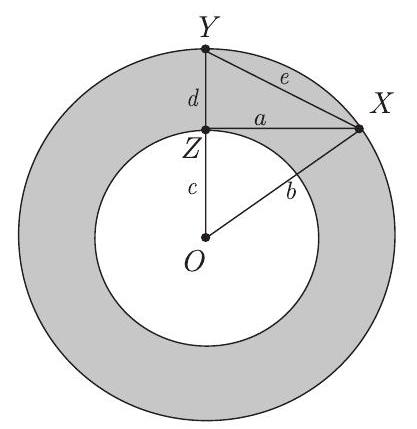
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: All the students in an algebra class took a -point test. Five students scored , each student scored at least , and the mean score was . What is the smallest possible number of students in the class?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: In the sequence , each term after the third is found by subtracting the previous term from the sum of the two terms that precede that term. For example, the fourth term is . What is the term in this sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If and with and real, what is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: In and . Points and lie on and , respectively, with . Points and are on so that and are perpendicular to . What is the area of pentagon ?
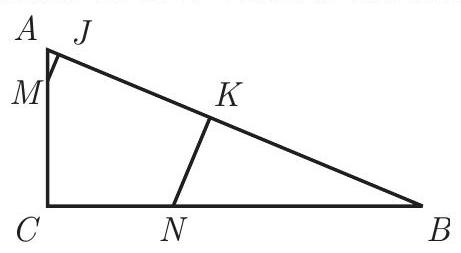
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The two digits in Jack's age are the same as the digits in Bill's age, but in reverse order. In five years Jack will be twice as old as Bill will be then. What is the difference in their current ages?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A function is defined by , where and is the complex conjugate of . How many values of satisfy both and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: For some real numbers and , the equation
has three distinct positive roots. If the sum of the base- logarithms of the roots is , what is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Points and are on the parabola , and the origin is the midpoint of . What is the length of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A truncated cone has horizontal bases with radii and . A sphere is tangent to the top, bottom, and lateral surface of the truncated cone. What is the radius of the sphere?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Each face of a cube is painted either red or blue, each with probability . The color of each face is determined independently. What is the probability that the painted cube can be placed on a horizontal surface so that the four vertical faces are all the same color?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The graph of is an ellipse in the first quadrant of the -plane. Let and be the maximum and minimum values of over all points on the ellipse. What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The square
is a multiplicative magic square. That is, the product of the numbers in each row, column, and diagonal is the same. If all the entries are positive integers, what is the sum of the possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The polynomial has integer coefficients and three distinct positive zeros. Exactly one of these is an integer, and it is the sum of the other two. How many values of are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: In , and is an altitude. Point is on the extension of such that . The values of , and form a geometric progression, and the values of form an arithmetic progression. What is the area of ?
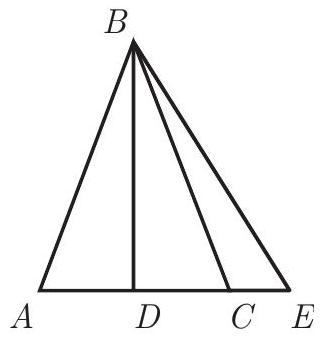
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Given that is a -digit number whose first digit is , how many elements of the set have a first digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions