¶ 2005 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2005 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2005 AMC 12A math contest by visiting Random Math AMC 12A 2005 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2005 AMC 12A problems, please refer below:
Problem 1: Two is of and of . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The equations and have the same solution for . What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A rectangle with a diagonal of length is twice as long as it is wide. What is the area of the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A store normally sells windows at each. This week the store is offering one free window for each purchase of four. Dave needs seven windows and Doug needs eight windows. How many dollars will they save if they purchase the windows together rather than separately?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The average (mean) of numbers is , and the average of other numbers is . What is the average of all numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Josh and Mike live miles apart. Yesterday Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Square is inside square so that each side of can be extended to pass through a vertex of . Square has side length is between and , and . What is the area of the inner square ?
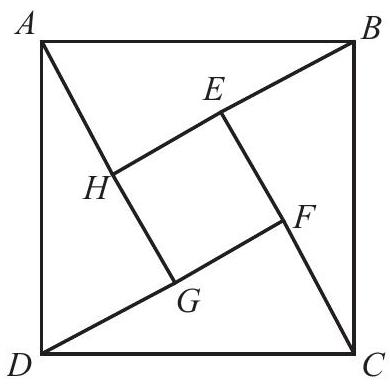
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let , and be digits with
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: There are two values of for which the equation has only one solution for . What is the sum of those values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A wooden cube units on a side is painted red on all six faces and then cut into unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A line passes through and . How many other points with integer coordinates are on the line and strictly between and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: In the five-sided star shown, the letters and are replaced by the numbers and , although not necessarily in that order. The sums of the numbers at the ends of the line segments and form an arithmetic sequence, although not necessarily in that order. What is the middle term of the arithmetic sequence?
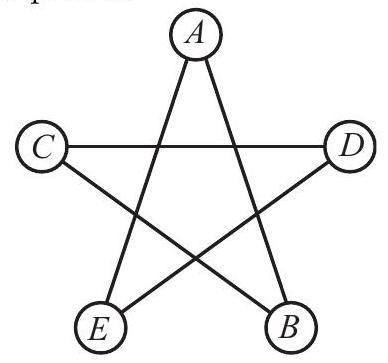
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: On a standard die one of the dots is removed at random with each dot equally likely to be chosen. The die is then rolled. What is the probability that the top face has an odd number of dots?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let be a diameter of a circle and be a point on with . Let and be points on the circle such that and is a second diameter. What is the ratio of the area of to the area of ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Three circles of radius are drawn in the first quadrant of the -plane. The first circle is tangent to both axes, the second is tangent to the first circle and the -axis, and the third is tangent to the first circle and the -axis. A circle of radius is tangent to both axes and to the second and third circles. What is ?
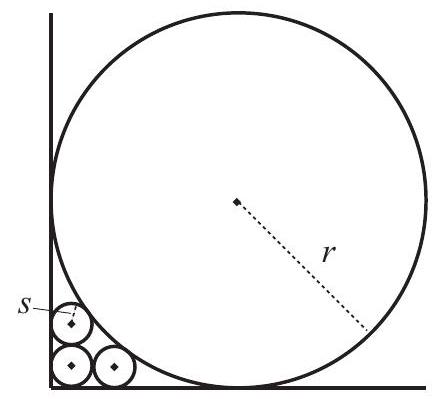
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A unit cube is cut twice to form three triangular prisms, two of which are congruent, as shown in Figure . The cube is then cut in the same manner along the dashed lines shown in Figure . This creates nine pieces. What is the volume of the piece that contains vertex ?
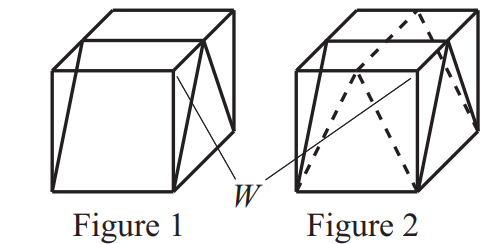
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Call a number "prime-looking" if it is composite but not divisible by , or . The three smallest prime-looking numbers are , and . There are prime numbers less than . How many prime-looking numbers are there less than ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A faulty car odometer proceeds from digit to digit , always skipping the digit , regardless of position. For example, after traveling one mile the odometer changed from to . If the odometer now reads , how many miles has the car actually traveled?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: For each in , define
Let , and for each integer . For how many values of in is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: How many ordered triples of integers , with , and , satisfy both and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A rectangular box is inscribed in a sphere of radius . The surface area of is , and the sum of the lengths of its edges is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Two distinct numbers and are chosen randomly from the set . What is the probability that is an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let . For how many polynomials does there exist a polynomial of degree such that ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be the set of all points with coordinates , where , and are each chosen from the set . How many equilateral triangles have all their vertices in ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions