¶ 2013 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2013 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2013 AMC 12A math contest by visiting Random Math AMC 12A 2013 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2013 AMC 12A problems, please refer below:
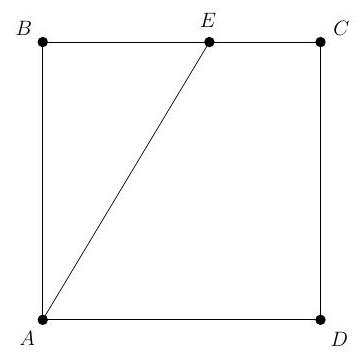
Problem 1: Square has side length . Point is on , and the area of is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A softball team played ten games, scoring , and runs. They lost by one run in exactly five games. In each of their other games, they scored twice as many runs as their opponent. How many total runs did their opponents score?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A flower bouquet contains pink roses, red roses, pink carnations, and red carnations. One third of the pink flowers are roses, three fourths of the red flowers are carnations, and six tenths of the flowers are pink. What percent of the flowers are carnations?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Tom, Dorothy, and Sammy went on a vacation and agreed to split the costs evenly. During their trip Tom paid , Dorothy paid , and Sammy paid . In order to share the costs equally, Tom gave Sammy dollars, and Dorothy gave Sammy dollars. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In a recent basketball game, Shenille attempted only three-point shots and two-point shots. She was successful on of her three-point shots and of her two-point shots. Shenille attempted shots. How many points did she score?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The sequence has the property that every term beginning with the third is the sum of the previous two. That is,
Suppose that and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Given that and are distinct nonzero real numbers such that , what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
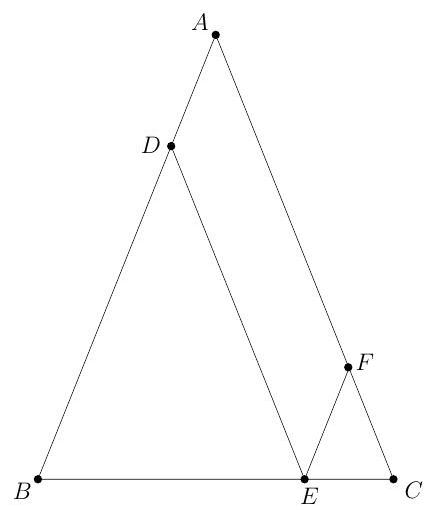
Problem 9: In and . Points , and are on sides , , and , respectively, such that and are parallel to and , respectively. What is the perimeter of parallelogram ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Let be the set of positive integers for which has the repeating decimal representation , with and different digits. What is the sum of the elements of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
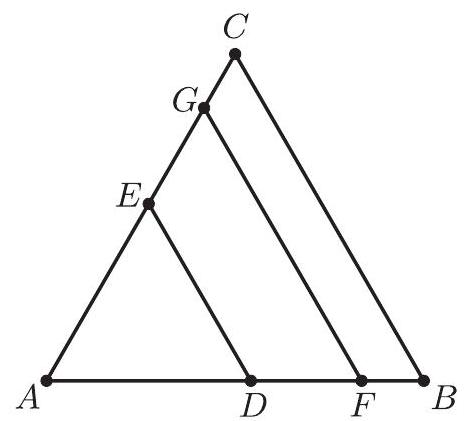
Problem 11: Triangle is equilateral with . Points and are on and points and are on such that both and are parallel to . Furthermore, triangle and trapezoids and all have the same perimeter. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The angles in a particular triangle are in arithmetic progression, and the side lengths are , and . The sum of the possible values of equals , where , and are positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Let points , and . Quadrilateral is cut into equal area pieces by a line passing through . This line intersects at point , where these fractions are in lowest terms. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The sequence
is an arithmetic progression. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Rabbits Peter and Pauline have three offspring-Flopsie, Mopsie, and Cottontail. These five rabbits are to be distributed to four different pet stores so that no store gets both a parent and a child. It is not required that every store gets a rabbit. In how many different ways can this be done?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: , and are three piles of rocks. The mean weight of the rocks in is pounds, the mean weight of the rocks in is pounds, the mean weight of the rocks in the combined piles and is pounds, and the mean weight of the rocks in the combined piles and is pounds. What is the greatest possible integer value for the mean in pounds of the rocks in the combined piles and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A group of pirates agree to divide a treasure chest of gold coins among themselves as follows. The pirate to take a share takes of the coins that remain in the chest. The number of coins initially in the chest is the smallest number for which this arrangement will allow each pirate to receive a positive whole number of coins. How many coins does the pirate receive?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Six spheres of radius are positioned so that their centers are at the vertices of a regular hexagon of side length . The six spheres are internally tangent to a larger sphere whose center is the center of the hexagon. An eighth sphere is externally tangent to the six smaller spheres and internally tangent to the larger sphere. What is the radius of this eighth sphere?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In , and . A circle with center and radius intersects at points and . Moreover and have integer lengths. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let be the set . For , define to mean that either or . How many ordered triples of elements of have the property that , and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Consider
Which of the following intervals contains ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A palindrome is a nonnegative integer number that reads the same forwards and backwards when written in base with no leading zeros. A -digit palindrome is chosen uniformly at random. What is the probability that is also a palindrome?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: is a square of side length . Point is on such that . The square region bounded by is rotated counterclockwise with center , sweeping out a region whose area is , where , and are positive integers and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Three distinct segments are chosen at random among the segments whose endpoints are the vertices of a regular -gon. What is the probability that the lengths of these three segments are the three side lengths of a triangle with positive area?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be defined by . How many complex numbers are there such that and both the real and the imaginary parts of are integers with absolute value at most ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions