¶ 2012 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2012 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2012 AMC 12B math contest by visiting Random Math AMC 12B 2012 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2012 AMC 12B problems, please refer below:
Problem 1: Each third-grade classroom at Pearl Creek Elementary has students and pet rabbits. How many more students than rabbits are there in all of the third-grade classrooms?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A circle of radius is inscribed in a rectangle as shown. The ratio of the length of the rectangle to its width is . What is the area of the rectangle?
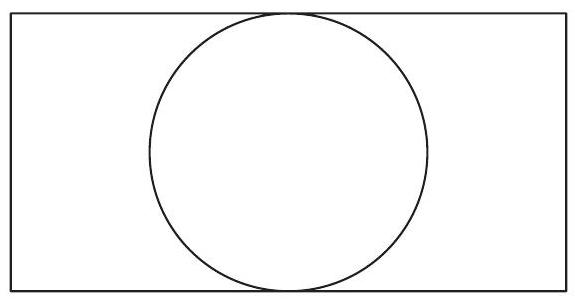
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: For a science project, Sammy observed a chipmunk and a squirrel stashing acorns in holes. The chipmunk hid acorns in each of the holes it dug. The squirrel hid acorns in each of the holes it dug. They each hid the same number of acorns, although the squirrel needed fewer holes. How many acorns did the chipmunk hide?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Suppose that the euro is worth dollars. If Diana has dollars and Etienne has euros, by what percent is the value of Etienne's money greater than the value of Diana's money?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Two integers have a sum of . When two more integers are added to the first two integers the sum is . Finally when two more integers are added to the sum of the previous four integers the sum is . What is the minimum number of even integers among the integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In order to estimate the value of where and are real numbers with , Xiaoli rounded up by a small amount, rounded down by the same amount, and then subtracted her rounded values. Which of the following statements is necessarily correct?
Answer Choices:
A. Her estimate is larger than .
B. Her estimate is smaller than .
C. Her estimate equals .
D. Her estimate equals .
E. Her estimate is 0 .
Solution:
Problem 7: Small lights are hung on a string inches apart in the order red, red, green, green, green, red, red, green, green, green, and so on continuing this pattern of red lights followed by green lights. How many feet separate the rd red light and the st red light?
Note: foot is equal to inches.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A dessert chef prepares the dessert for every day of a week starting with Sunday. The dessert each day is either cake, pie, ice cream, or pudding. The same dessert may not be served two days in a row. There must be cake on Friday because of a birthday. How many different dessert menus for the week are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: It takes Clea seconds to walk down an escalator when it is not operating, and only seconds to walk down the escalator when it is operating. How many seconds does it take Clea to ride down the operating escalator when she just stands on it?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: What is the area of the polygon whose vertices are the points of intersection of the curves and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: In the equation below, and are consecutive positive integers, and , and represent number bases:
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: How many sequences of zeros and/or ones of length have all the zeros consecutive, or all the ones consecutive, or both?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Two parabolas have equations and , where , , and are integers (not necessarily different), each chosen independently by rolling a fair six-sided die. What is the probability that the parabolas have at least one point in common?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Bernardo and Silvia play the following game. An integer between and , inclusive, is selected and given to Bernardo. Whenever Bernardo receives a number, he doubles it and passes the result to Silvia. Whenever Silvia receives a number, she adds to it and passes the result to Bernardo. The winner is the last person who produces a number less than . Let be the smallest initial number that results in a win for Bernardo. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Jesse cuts a circular paper disk of radius along two radii to form two sectors, the smaller having a central angle of degrees. He makes two circular cones, using each sector to form the lateral surface of a cone. What is the ratio of the volume of the smaller cone to that of the larger?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Amy, Beth, and Jo listen to four different songs and discuss which ones they like. No song is liked by all three. Furthermore, for each of the three pairs of the girls, there is at least one song liked by those two girls but disliked by the third. In how many different ways is this possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Square lies in the first quadrant. Points , and lie on lines , and , respectively. What is the sum of the coordinates of the center of the square ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be a list of the first 10 positive integers such that for each either or or both appear somewhere before in the list. How many such lists are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A unit cube has vertices , and . Vertices , and are adjacent to , and for , vertices and are opposite to each other. A regular octahedron has one vertex in each of the segments , , and . What is the octahedron's side length?
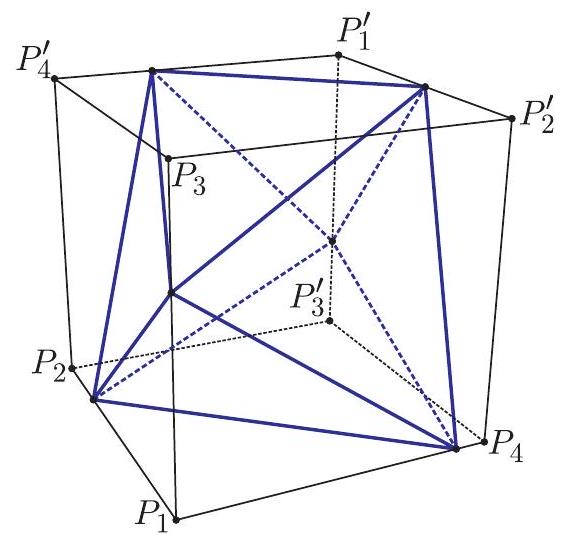
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A trapezoid has side lengths , and 11 . The sum of all the possible areas of the trapezoid can be written in the form of , where , and are rational numbers and and are positive integers not divisible by the square of a prime. What is the greatest integer less than or equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Square is inscribed in equiangular hexagon with on , on , and on . Suppose that and . What is the side-length of the square?
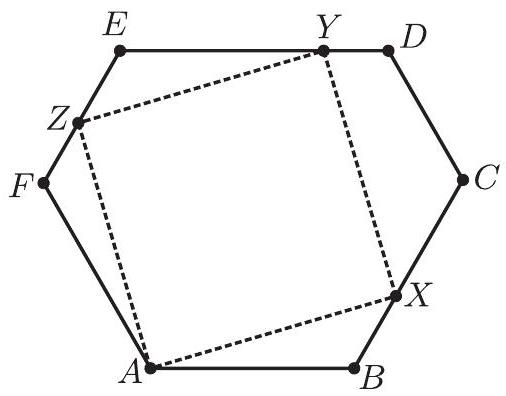
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A bug travels from to along the segments in the hexagonal lattice pictured below. The segments marked with an arrow can be traveled only in the direction of the arrow, and the bug never travels the same segment more than once. How many different paths are there?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Consider all polynomials of a complex variable, , where , and are integers, , and the polynomial has a zero with . What is the sum of all values over all the polynomials with these properties?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Define the function on the positive integers by setting and if is the prime factorization of , then
For every , let . For how many in the range is the sequence unbounded?
Note: a sequence of positive numbers is unbounded if for every integer , there is a member of the sequence greater than .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let , and . Let be the set of all right triangles whose vertices are in . For every right triangle with vertices , and in counter-clockwise order and right angle at , let . What is
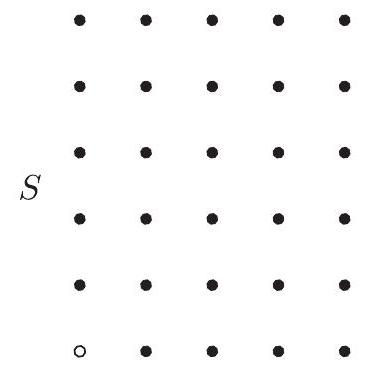
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions