¶ 2019 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2019 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2019 AMC 12A math contest by visiting Random Math AMC 12A 2019 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2019 AMC 12A problems, please refer below:
Problem 1: The area of a pizza with radius inches is percent larger than the area of a pizza with radius inches. What is the integer closest to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Suppose is of . What percent of is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A box contains red balls, green balls, yellow balls, blue balls, white balls, and black balls. What is the minimum number of balls that must be drawn from the box without replacement to guarantee that at least balls of a single color will be drawn?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: What is the greatest number of consecutive integers whose sum is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Two lines with slopes and intersect at . What is the area of the triangle enclosed by these two lines and the line ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The figure below shows line with a regular, infinite, recurring pattern of squares and line segments.
How many of the following four kinds of rigid motion transformations of the plane in which this figure is drawn, other than the identity transformation, will transform this figure into itself?
-
some rotation around a point of line
-
some translation in the direction parallel to line
-
the reflection across line
-
some reflection across a line perpendicular to line

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Melanie computes the mean , the median , and the modes of the values that are the dates in the months of . Thus her data consist of , and . Let be the median of the modes. Which of the following statements is true?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: For a set of four distinct lines in a plane, there are exactly distinct points that lie on two or more of the lines. What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A sequence of numbers is defined recursively by , and
for all Then can be written as , where and are relatively prime positive inegers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The figure below shows circles of radius within a larger circle. All the intersections occur at points of tangency. What is the area of the region, shaded in the figure, inside the larger circle but outside all the circles of radius ?
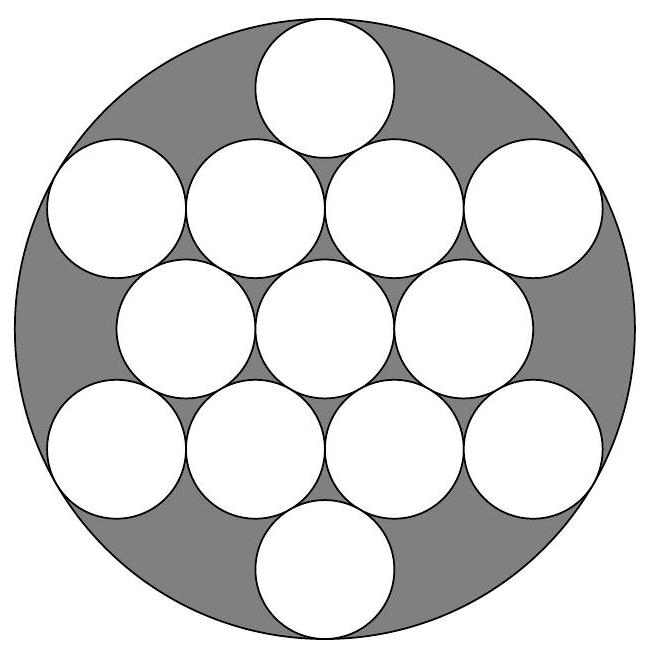
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: For some positive integer , the repeating base- representation of the (base-ten) fraction is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Positive real numbers and satisfy and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many ways are there to paint each of the integers either red, green, or blue so that each number has a different color from each of its proper divisors?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: For a certain complex number , the polynomial
has exactly distinct roots. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Positive real numbers and have the property that
and all four terms on the left are positive integers, where log denotes the base logarithm. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The numbers are randomly placed into the squares of a grid. Each square gets one number, and each of the numbers is used once. What is the probability that the sum of the numbers in each row and each column is odd?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let denote the sum of the th powers of the roots of the polynomial . In particular, , and . Let , and be real numbers such that for What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A sphere with center has radius . A triangle with sides of length , and is situated in space so that each of its sides is tangent to the sphere. What is the distance between and the plane determined by the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In with integer side lengths,
What is the least possible perimeter for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Real numbers between and , inclusive, are chosen in the following manner. A fair coin is flipped. If it lands heads, then it is flipped again and the chosen number is if the second flip is heads and if the second flip is tails. On the other hand, if the first coin flip is tails, then the number is chosen uniformly at random from the closed interval . Two random numbers and are chosen independently in this manner. What is the probability that ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Circles and , both centered at , have radii and , respectively. Equilateral triangle , whose interior lies in the interior of but in the exterior of , has vertex on , and the line containing side is tangent to . Segments and intersect at , and . Then can be written in the form for positive integers with . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Define binary operations and by
for all real numbers and for which these expressions are defined. The sequence is defined recursively by and
for all integers . To the nearest integer, what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: For how many integers between and , inclusive, is
an integer? (Recall that .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a triangle whose angle measures are exactly , and . For each positive integer define to be the foot of the altitude from to line . Likewise, define to be the foot of the altitude from to line , and to be the foot of the altitude from to line . What is the least positive integer for which is obtuse?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions