¶ 2018 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2018 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2018 AMC 12B math contest by visiting Random Math AMC 12B 2018 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2018 AMC 12B problems, please refer below:
Problem 1: Kate bakes a -inch by -inch pan of cornbread. The cornbread is cut into pieces that measure inches by inches. How many pieces of cornbread does the pan contain?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Sam drove miles in minutes. His average speed during the first minutes was (miles per hour), and his average speed during the second minutes was . What was his average speed, in mph, during the last minutes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A circle has a chord of length , and the distance from the center of the circle to the chord is . What is the area of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: How many subsets of contain at least one prime number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Suppose cans of soda can be purchased from a vending machine for quarters. Which of the following expressions describes the number of cans of soda that can be purchased for dollars, where dollar is worth quarters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Line segment is a diameter of a circle with . Point , not equal to or , lies on the circle. As point moves around the circle, the centroid (center of mass) of traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A list of positive integers has a unique mode, which occurs exactly times. What is the least number of distinct values that can occur in the list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper, as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box, point in the figure on the right. The box has base length and height . What is the area of the sheet of wrapping paper?
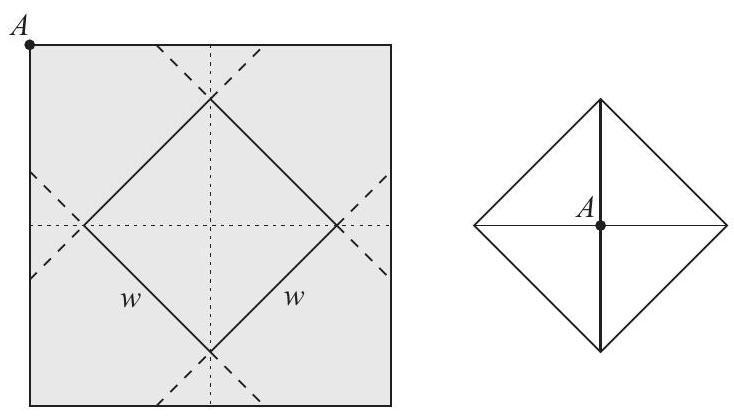
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Side of has length . The bisector of angle meets at , and . The set of all possible values of is an open interval . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Square has side length 30 . Point lies inside the square so that and . The centroids of , , and are the vertices of a convex quadrilateral. What is the area of that quadrilateral?
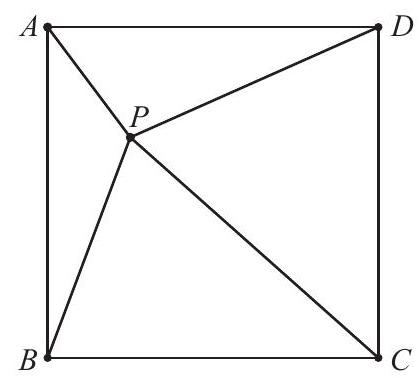
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Joey and Chloe and their daughter Zoe all have the same birthday. Joey is year older than Chloe, and Zoe is exactly year old today. Today is the first of the birthdays on which Chloe's age will be an integral multiple of Zoe's age. What will be the sum of the two digits of Joey's age the next time his age is a multiple of Zoe's age?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: How many -digit positive odd multiples of do not include the digit ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The solutions to the equation are connected in the complex plane to form a convex regular polygon, three of whose vertices are labeled , and . What is the least possible area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let and be positive integers such that
and is as small as possible. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A function is defined recursively by and
for all integers . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Mary chose an even -digit number . She wrote down all the divisors of in increasing order from left to right: . At some moment Mary wrote as a divisor of . What is the smallest possible value of the next divisor written to the right of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let be a regular hexagon with side length . Denote by , , and the midpoints of sides , and , respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: In with side lengths , and , let and denote the circumcenter and incenter, respectively. A circle with center is tangent to the legs and and to the circumcircle of . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Consider polynomials of degree at most , each of whose coefficients is an element of . How many such polynomials satisfy ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Ajay is standing at point near Pontianak, Indonesia, latitude and longitude. Billy is standing at point near Big Baldy Mountain, Idaho, USA, latitude and longitude. Assume that Earth is a perfect sphere with center . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let denote the greatest integer less than or equal to . How many real numbers satisfy the equation ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Circles , and each have radius 4 and are placed in the plane so that each circle is externally tangent to the other two. Points , , and lie on , and , respectively, so that and line is tangent to for each , where . See the figure below. The area of can be written in the form , where and are positive integers. What is ?
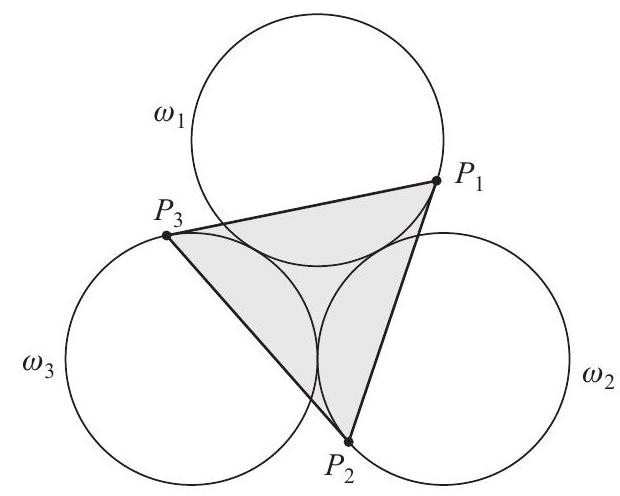
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions