¶ 2019 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2019 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2019 AMC 12B math contest by visiting Random Math AMC 12B 2019 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2019 AMC 12B problems, please refer below:
Problem 1: Alicia had two containers. The first was full of water and the second was empty. She poured all the water from the first container into the second container, at which point the second
container was full of water. What is the ratio of the volume of the first container to the volume of the second container?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Consider the statement, "If is not prime, then is prime." Which of the following values of is a counterexample to this statement?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Which one of the following rigid transformations (isometries) maps the line segment onto the line segment so that the image of is and the image of is ?
Answer Choices:
A. reflection in the -axis
B. counterclockwise rotation around the origin by
C. translation by units to the right and units down
D. reflection in the -axis
E. clockwise rotation about the origin by
Solution:
Problem 4: A positive integer satisfies the equation . What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Each piece of candy in a store costs a whole number of cents. Casper has exactly enough money to buy either pieces of red candy, pieces of green candy, pieces of blue candy, or pieces of purple candy. A piece of purple candy costs cents. What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In a given plane, points and are units apart. How many points are there in the plane such that the perimeter of is units and the area of is square units?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 7: What is the sum of all real numbers for which the median of the numbers , and is equal to the mean of those five numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let . What is the value of the sum
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: For how many integral values of can a triangle of positive area be formed having side lengths ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The figure below is a map showing cities and roads connecting certain pairs of cities. Paula wishes to travel along exactly of those roads, starting at city and ending at city , without traveling along any portion of a road more than once. (Paula is allowed to visit a city more than once.) How many different routes can Paula take?
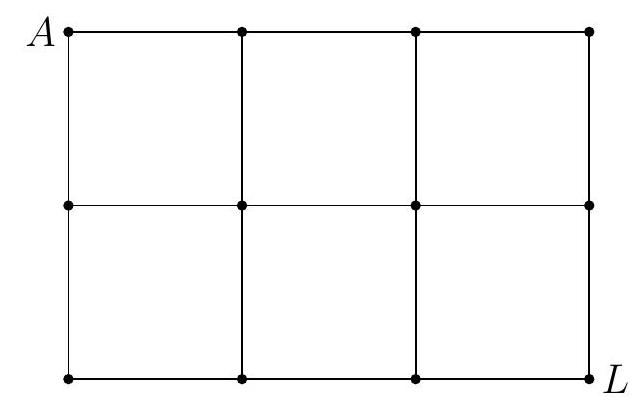
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: How many unordered pairs of edges of a given cube determine a plane?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Right triangle with right angle at is constructed outwards on the hypotenuse of isosceles right triangle with leg length , as shown, so that the two triangles have equal perimeters. What is ?
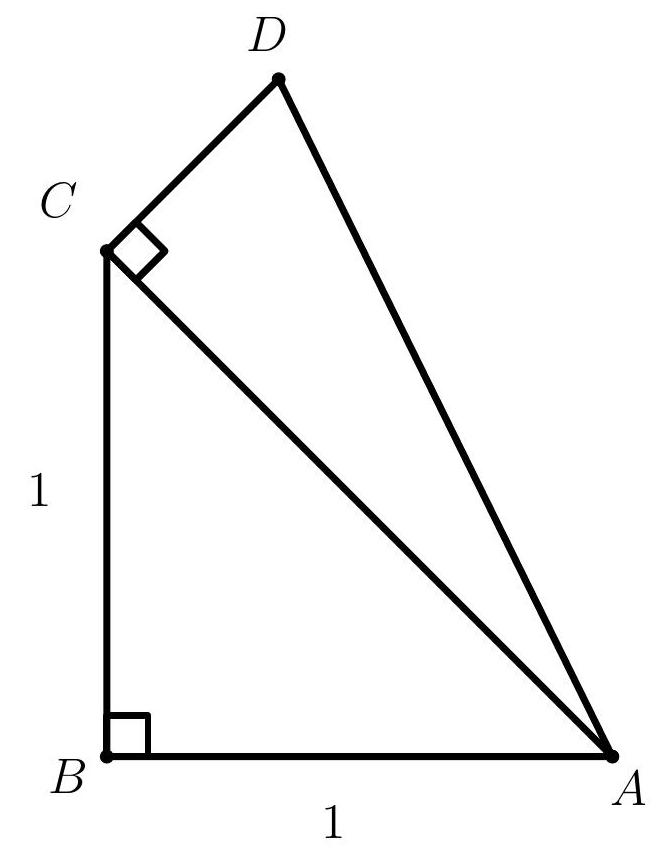
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A red ball and a green ball are randomly and independently tossed into bins numbered with positive integers so that for each ball, the probability that it is tossed into bin is for What is the probability that the red ball is tossed into a higher-numbered bin than the green ball?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Let be the set of all positive integer divisors of . How many numbers are the product of two distinct elements of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: As shown in the figure, line segment is trisected by points and so that . Three semicircles of radius , and , have their diameters on , and are tangent to line at , and , respectively. A circle of radius 2 has its center on . The area of the region inside the circle but outside the three semicircles, shaded in the figure, can be expressed in the form
where , and are positive integers and and are relatively prime. What is ?
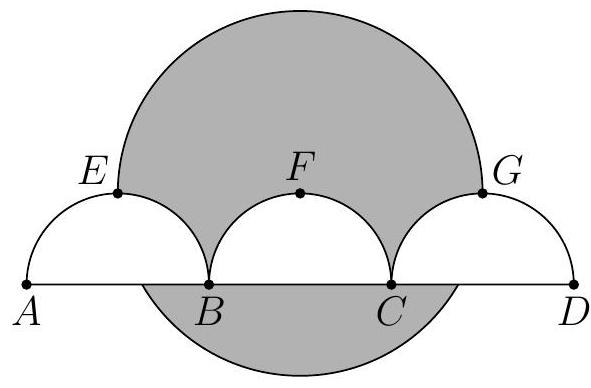
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: There are lily pads in a row numbered to , in that order. There are predators on lily pads and , and a morsel of food on lily pad . Fiona the frog starts on pad , and from any given lily pad, has a chance to hop to the next pad, and an equal chance to jump pads. What is the probability that Fiona reaches pad without landing on either pad or pad ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: How many nonzero complex numbers have the property that , and , when represented by points in the complex plane, are the three distinct vertices of an equilateral triangle?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 18: Square pyramid has base , which measures on a side, and altitude perpendicular to the base, which measures . Point lies on , one third of the way from to ; point lies on , one third of the way from to ; and point lies on , two thirds of the way from to . What is the area, in square centimeters, of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Raashan, Sylvia, and Ted play the following game. Each starts with . A bell rings every seconds, at which time each of the players who currently have money simultaneously chooses one of the other two players independently and at random and gives to that player. What is the probability that after the bell has rung times, each player will have ? (For example, Raashan and Ted may each decide to give to Sylvia, and Sylvia may decide to give her dollar to Ted, at which point Raashan will have , Sylvia would have , and Ted would have , and and that is the end of the first round of play. In the second round Raashan has no money to give, but Sylvia and Ted might choose each other to give their to, and and the holdings will be the same as the end of the second [sic] round.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Points and lie on circle in the plane. Suppose that the tangent lines to at and intersect at a point on the -axis. What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: How many quadratic polynomials with real coefficients are there such that the set of roots equals the set of coefficients? (For clarification: If the polynomial is , and the roots are and , then the requirement is that .)
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 22: Define a sequence recursively by and
for all nonnegative integers . Let be the least positive integer such that
In which of the following intervals does lie?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: How many sequences of s and s of length are there that begin with a , end with a , contain no two consecutive s, and contain no three consecutive ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let . Let denote all points in the complex plane of the form , where , and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a convex quadrilateral with and . Suppose that the centroids of , and form the vertices of an equilateral triangle. What is the maximum possible value of the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions