¶ 1993 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1993 AMC8 problems here.
Discussion Forum
Engage in discussion about the 1993 AMC8 math contest by visiting Random Math 1993 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1993 AMC8 problems, please refer below:
Problem 1: Which pair of numbers does NOT have a product equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: When the fraction is expressed in simplest form, then the sum of the numerator and the denominator will be
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Which of the following numbers has the largest prime factor?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Which one of the following bar graphs could represent the data from the circle graph?
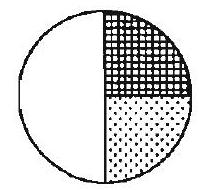
Answer Choices:
A.
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
Solution:
Problem 6: A can of soup can feed adults or children. If there are cans of soup and children are fed, then how many adults would the remaining soup feed?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: To control her blood pressure, Jill's grandmother takes one half of a pill every other day. If one supply of medicine contains pills, then the supply of medicine will last approximately
Answer Choices:
A. month
B. month
C. month
D. month
E. year
Solution:
Problem 9: Consider the operation * defined by the following table:
For example, . Then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: This line graph represents the price of a trading card during the first months of .The greatest monthly drop in price occurred during
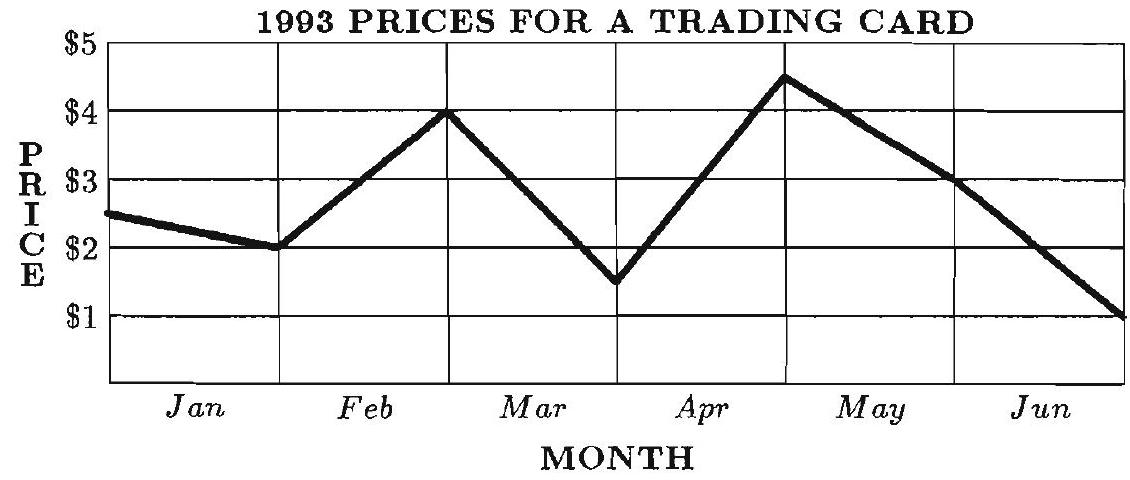
Answer Choices:
A. January
B. March
C. April
D. May
E. June
Solution:
Problem 11: Consider this histogram of the scores for students taking a test:
.jpg)
The median is in the interval labeled
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If each of the three operation signs is used exactly ONCE in one of the blanks in the expression
then the value of the result could equal
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The word in block letters is painted in black with strokes unit wide on a by rectangular white sign with dimensions as shown. The area of the white portion of the sign, in square units, is
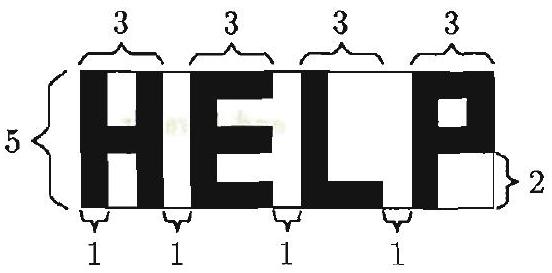
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The nine squares in the table shown are to be filled so that every row and every column contains each of the numbers . Then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The arithmetic mean (average) of four numbers is . If the largest of these numbers is , then the mean of the remaining three numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Square corners, units on a side, are removed from a unit by unit rectangular sheet of cardboard. The sides are then folded to form an open box. The surface area, in square units, of the interior of the box is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The rectangle shown has length , width , and and are midpoints of and , respectively. The area of the quadrilateral is
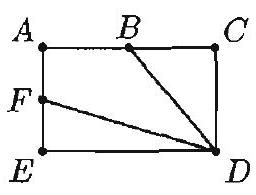
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: When is expressed as a single whole number, the sum of the digits is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If the length of a rectangle is increased by and its width is increased by , then the area is increased by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Pat Peano has plenty of and , but he has only twenty-two . How far can he number the pages of his scrapbook with these digits?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Five runners, , have a race, and beats beats beats , and finishes after and before . Who could NOT have finished third in the race?
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 24: What number is directly above in this array of numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A checkerboard consists of one-inch squares. A square card, inches on a side, is placed on the board so that it covers part or all of the area of each of squares. The maximum possible value of is
Answer Choices:
A. or
B. or
C. or
D. or
E. or more
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions