¶ 1996 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1996 AMC8 problems here.
Discussion Forum
Engage in discussion about the 1996 AMC8 math contest by visiting Random Math 1996 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1996 AMC8 problems, please refer below:
Problem 1: How many positive factors of are also multiples of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: José, Thuy, and Kareem each start with the number . José subtracts from the number , doubles his answer, and then adds . Thuy doubles the number , subtracts from her answer, and then adds . Kareem subtracts from the number , adds to his answer, and then doubles the result. Who gets the largest final answer?
Answer Choices:
A. José
B. Thuy
C. Kareem
D. José and Thuy
E. Thuy and Kareem
Solution:
Problem 3: The whole numbers from through are written, one per square, on a checkerboard (an by array of squares). The first numbers are written in order across the first row, the next across the second row, and so on. After all numbers are written, the sum of the numbers in the four corners will be
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The letters , and represent numbers located on the number line as shown.
Which of the following expressions represents a negative number?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: What is the smallest result that can be obtained by the following process?
-
Choose three different numbers from the set .
-
Add two of these numbers.
-
Multiply their sum by the third number.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Brent has goldfish that quadruple (become four times as many) every month, and Gretel has goldfish that double every month. If Brent has goldfish at the same time that Gretel has goldfish, then in how many months from that time will they have the same number of goldfish?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Points and are units apart. Points and are units apart. Points and are units apart. If and are as close as possible, then the number of units between them is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: If times a number is , then times the reciprocal of the number is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: When Walter drove up to the gasoline pump, he noticed that his gasoline tank was full. He purchased gallons of gasoline for . With this additional gasoline, his gasoline tank was then full. The number of gallons of gasoline his tank holds when it is full is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Let be the number
where there are zeros after the decimal point. Which of the following expressions represents the largest number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: What number should be removed from the list
so that the average of the remaining numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: In the fall of , a total of students participated in an annual school clean-up day. The organizers of the event expect that in each of the years , and , participation will increase by over the previous year. The number of participants the organizers expect in the fall of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Six different digits from the set
are placed in the squares in the figure shown so that the sum of the entries in the vertical column is and the sum of the entries in the horizontal row is . The sum of the six digits used is
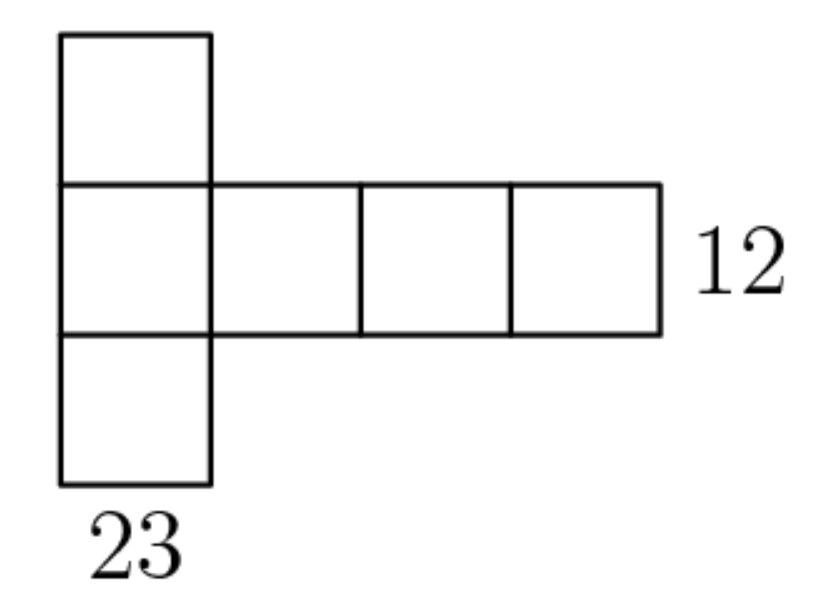
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The remainder when the product is divided by is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Figure is a square. Point is the origin, and point has coordinates . What are the coordinates for so that the area of triangle equals the area of square
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Ana's monthly salary was in May. In June she received a raise. In July she received a pay cut. After the two changes in June and July, Ana's monthly salary was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The pie charts at the right indicate the percent of students who prefer golf, bowling, or tennis at East Junior High School and West Middle School. The total number of students at East is and at West, . In the two schools combined, the percent of students who prefer tennis is
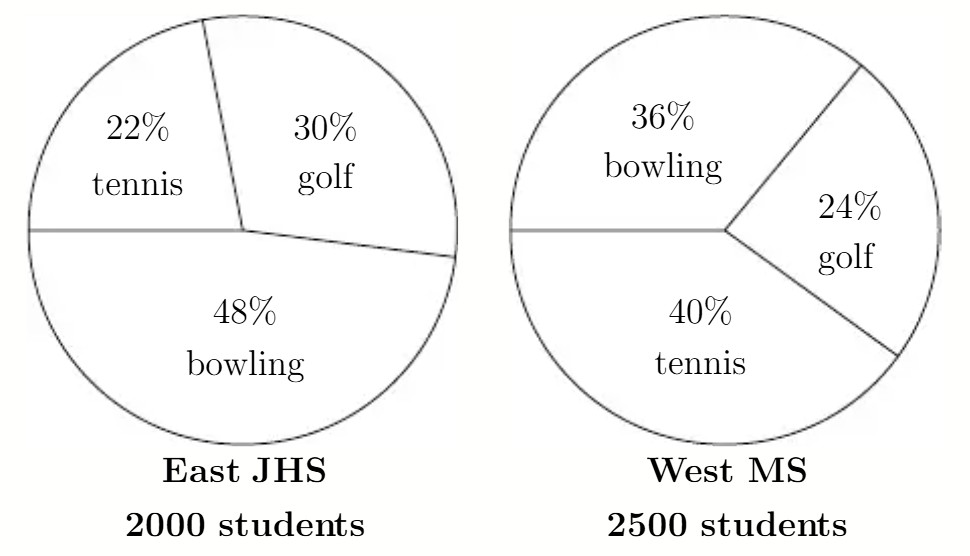
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Suppose there is a special key on a calculator that replaces the number currently displayed with the number given by the formula . For example, if the calculator is displaying and the special key is pressed, then the calculator will display since . Now suppose that the calculator is displaying . After the special key is pressed times in a row, the calculator will display
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: How many subsets containing three different numbers can be selected from the set
so that the sum of the three numbers is even?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The horizontal and vertical distances between adjacent points equal unit. The area of triangle is
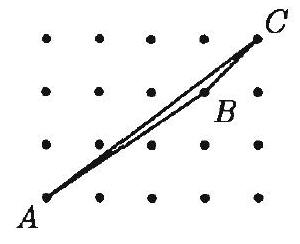
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The manager of a company planned to distribute a bonus to each employee from the company fund, but the fund contained less than what was needed. Instead the manager gave each employee a bonus and kept the remaining in the company fund. The amount of money in the company fund before any bonuses were paid was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The measure of angle is , bisects angle , and bisects angle . The measure of angle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A point is chosen at random from within a circular region. What is the probability that the point is closer to the center of the region than it is to the boundary of the region?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions