¶ 1997 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1997 AMC8 problems here.
Discussion Forum
Engage in discussion about the 1997 AMC8 math contest by visiting Random Math 1997 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1997 AMC8 problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Ahn chooses a two-digit number, subtracts it from , and doubles the result. What is the largest number Ahn can get?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Which of the following numbers is the largest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Julie is preparing a speech for her class. Her speech must last between one-half hour and three-quarters of an hour. The ideal rate of speech is words per minute. If Julie speaks at the ideal rate, which of the following number of words would be an appropriate length for her speech?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: There are many two-digit multiples of , but only two of the multiples have a digit sum of . The sum of these two multiples of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In the number the value of the place occupied by the digit is how many times as great as the value of the place occupied by the digit
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The area of the smallest square that will contain a circle of radius is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Walter gets up at a.m., catches the school bus at a.m., has classes that last minutes each, has minutes for lunch, and has hours additional time at school. He takes the bus home and arrives at p.m. How many minutes has he spent on the bus?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Three students, with different names, line up single file. What is the probability that they are in alphabetical order from front-to-back?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: What fraction of this square region is shaded? Stripes are equal in width, and the figure is drawn to scale.

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Let mean the number of whole number divisors of . For example, , because has two divisors, and . Find the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: .
.
Find .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Three bags of jelly beans contain , and beans. The ratios of yellow beans to all beans in each of these bags are , and , respectively. All three bags of candy are dumped into one bowl. Which of the following is closest to the ratio of yellow jelly beans to all beans in the bowl?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: There is a set of five positive integers whose average (mean) is , whose median is , and whose only mode is . What is the difference between the largest and smallest integers in the set?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Each side of the large square in the figure is trisected (divided into three equal parts). The corners of an inscribed square are at these trisection points, as shown. The ratio of the area of the inscribed square to the area of the large square is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Penni Precisely buys worth of stock in each of three companies: Alabama Almonds, Boston Beans, and California Cauliflower. After one year, was up , was down , and was unchanged. For the second year, was down from the previous year, was up from the previous year, and was unchanged. If , and are the final values of the stock, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A cube has eight vertices (corners) and twelve edges. A segment, such as , which joins two vertices not joined by an edge is called a diagonal. Segment y is also a diagonal. How many diagonals does a cube have?
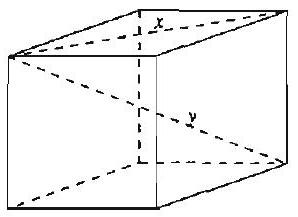
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: At the grocery store last week, small boxes of facial tissue were priced at boxes for . This week they are on sale at boxes for . The percent decrease in the price per box during the sale was closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: If the product , what is the sum of and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A pair of -sided dice have sides numbered through . Each side has the same probability (chance) of landing face up. The probability that the product of the two numbers on the sides that land face-up exceeds is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Each corner cube is removed from this cube. The surface area of the remaining figure is
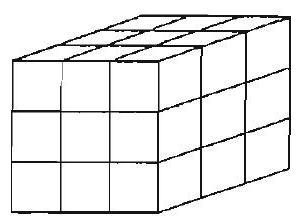
Answer Choices:
A. sq. cm
B. sq. cm
C. sq. cm
D. sq. cm
E. sq. cm
Solution:
Problem 22: A two-inch cube of silver weighs pounds and is worth . How much is a three-inch cube of silver worth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: There are positive integers that have these properties:
. the sum of the squares of their digits is , and
. each digit is larger than the one to its left.
The product of the digits of the largest integer with both properties is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: is divided at in the ratio . The two semicircles, and , divide the circular region into an upper (shaded) region and a lower region. The ratio of the area of the upper region to that of the lower region is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: All of the even numbers from to inclusive, except those ending in , are multiplied together. What is the rightmost digit (the units digit) of the product?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions