¶ 1998 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1998 AMC8 problems here.
Discussion Forum
Engage in discussion about the 1998 AMC8 math contest by visiting Random Math 1998 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1998 AMC8 problems, please refer below:
Problem 1: For , which of the following is smallest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If , what is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: How many triangles are in this figure? (Some triangles may overlap other triangles.)
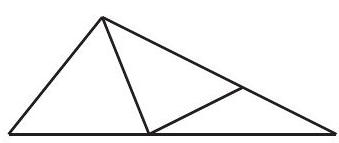
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Which of the following numbers is largest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Dots are spaced one unit part, horizontally and vertically. The number of square units enclosed by the polygon is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A child's wading pool contains gallons of water. If water evaporates at the rate of gallons per day and no other water is added or removed, how many gallons of water will be in the pool after days?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: For a sale, a store owner reduces the price of a scarf by . Later the price is lowered again, this time by one-half the reduced price. The price is now
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Each of the letters , and represents a different integer in the set , but not necessarily in that order. If , then the sum of and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Harry has sisters and brothers. His sister Harriet has sisters and brothers. What is the product of and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: What is the ratio of the area of the shaded square to the area of the large square? (The figure is drawn to scale.)
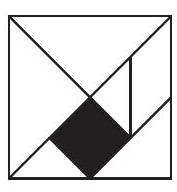
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: At Annville Junior High School, of the students in the Math Club are in the Science Club, and of the students in the Science Club are in the Math Club. There are students in the Science Club. How many students are in the Math Club?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: In the very center of the Irenic Sea lie the beautiful Nisos Isles. In the number of people on these islands is only , but the population triples every years. Queen Irene has decreed that there must be at least square miles for every person living in the Isles. The total area of the Nisos Isles is square miles.
Estimate the population of Nisos in the year .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In the very center of the Irenic Sea lie the beautiful Nisos Isles. In the number of people on these islands is only , but the population triples every years. Queen Irene has decreed that there must be at least square miles for every person living in the Isles. The total area of the Nisos Isles is square miles.
Estimate the year in which the population of Nisos will be approximately .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In the very center of the Irenic Sea lie the beautiful Nisos Isles. In the number of people on these islands is only , but the population triples every years. Queen Irene has decreed that there must be at least square miles for every person living in the Isles. The total area of the Nisos Isles is square miles.
In how many years, approximately, from will the population of Nisos be as much as Queen Irene has proclaimed that the islands can support?
Answer Choices:
A. yrs.
B. yrs.
C. yrs.
D. yrs.
E. yrs.
Solution:
Problem 18: As indicated by the diagram at the right, a rectangular piece of paper is folded bottom to top, then left to right, and finally, a hole is punched at . What does the paper look like when unfolded?
.jpg)
Answer Choices:
A.
.jpg)
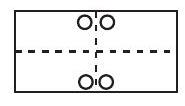
.jpg)
.jpg)
.jpg)
Solution:
Problem 19: Tamika selects two different numbers at random from the set and adds them. Carlos takes two different numbers at random from the set and multiplies them. What is the probability that Tamika's result is greater than Carlos' result?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let be a square piece of paper. is folded onto and then is folded onto . The area of the resulting figure is square inches. Find the perimeter of square .
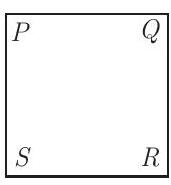
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A cubical box contains identical small cubes that exactly fill the box. How many of these small cubes touch a side or the bottom of the box?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Terri produces a sequence of positive integers by following three rules. She starts with a positive integer, then applies the appropriate rule to the result, and continues in this fashion.
Rule 1: If the integer is less than , multiply it by .
Rule 2: If the integer is even and greater than , divide it by .
Rule 3: If the integer is odd and greater than , subtract from it.
A sample sequence:
Find the term of the sequence that begins .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If the pattern in the diagram continues, what fraction of the interior would be shaded in the eighth triangle?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A rectangular board of columns has squares numbered beginning in the upper left corner and moving left to right so row one is numbered through , row two is through , and so on. A student shades square , then skips one square and shades square , skip two squares and shades square , ships squares and shades square , and continues in this way until there is at least one shaded square in each column. What is the number of the shaded square that first achieves this result?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Three generous friends, each with some cash, redistribute their money as follows: Ami gives enough money to Jan and Toy to double the amount that each has. Jan then gives enough to Ami and Toy to double their amounts. Finally, Toy gives Ami and Jan enough to double their amounts. If Toy has when they begin and when they end, what is the total amount that all three friends have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions