¶ 2005 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2005 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2005 AMC8 math contest by visiting Random Math 2005 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2005 AMC8 problems, please refer below:
Problem 1: Connie multiplies a number by and gets as her answer. However, she should have divided the number by to get the correct answer. What is the correct answer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Karl bought five folders from Pay-A-Lot at a cost of each. Pay-A-Lot had a 20%-off sale the following day. How much could Karl have saved on the purchase by waiting a day?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: What is the minimum number of small squares that must be colored black so that a line of symmetry lies on the diagonal of square
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A square and a triangle have equal perimeters. The lengths of the three sides of the triangle are and . What is the area of the square in square centimeters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Soda is sold in packs of and cans. What is the minimum number of packs needed to buy exactly cans of soda?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Suppose is a digit. For how many values of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Bill walks mile south, then mile east, and finally mile south. How many miles is he, in a direct line, from his starting point?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Suppose and are positive odd integers. Which of the following must also be an odd integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In quadrilateral , sides and both have length , sides and both have length , and the measure of angle is . What is the length of diagonal
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Joe had walked half way from home to school when he realized he was late. He ran the rest of the way to school. He ran times as fast as he walked. Joe took minutes to walk half way to school. How many minutes did it take Joe to get from home to school?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The sales tax rate in Bergville is . During a sale at the Bergville Coat Closet, the price of a coat is discounted from its price. Two clerks, Jack and Jill, calculate the bill independently. Jack rings up and adds sales tax, then subtracts from this total. Jill rings up , subtracts of the price, then adds of the discounted price for sales tax. What is Jack's total minus Jill's total?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Big Al, the ape, ate bananas from May through May . Each day he ate six more bananas than on the previous day. How many bananas did Big Al eat on May
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The area of polygon is with and . What is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The Little Twelve Basketball Conference has two divisions, with six teams in each division. Each team plays each of the other teams in its own division twice and every team in the other division once. How many conference games are scheduled?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: How many different isosceles triangles have integer side lengths and perimeter
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A five-legged Martian has a drawer full of socks, each of which is red, white or blue, and there are at least five socks of each color. The Martian pulls out one sock at a time without looking. How many socks must the Martian remove from the drawer to be certain there will be socks of the same color?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The results of a cross-country team's training run are graphed below. Which student has the greatest average speed?
.jpg)
Answer Choices:
A. Angela
B. Briana
C. Carla
D. Debra
E. Evelyn
Solution:
Problem 18: How many three-digit numbers are divisible by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
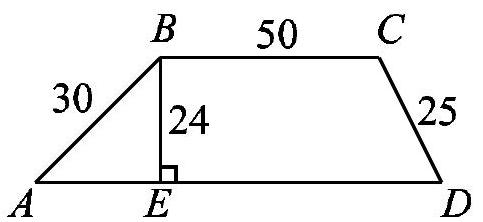
Problem 19: What is the perimeter of trapezoid
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Alice and Bob play a game involving a circle whose circumference is divided by equally-spaced points. The points are numbered clockwise, from to . Both start on point . Alice moves clockwise and Bob, counterclockwise. In a turn of the game, Alice moves points clockwise and Bob moves points counterclockwise. The game ends when they stop on the same point. How many turns will this take?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: How many distinct triangles can be drawn using three of the dots below as vertices?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A company sells detergent in three different sized boxes: small , medium and large . The medium size costs more than the small size and contains less detergent than the large size. The large size contains twice as much detergent as the small size and costs more than the medium size. Rank the three sizes from best to worst buy.
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Isosceles right triangle encloses a semicircle of area . The circle has its center on hypotenuse and is tangent to sides and . What is the area of triangle
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A certain calculator has only two keys: and . Each time you press one of these keys, the calculator automatically displays the result. For example, if the calculator initially displays "" and you press , it will display "". If you then press , it will display "". Starting with the display "", what is the fewest number of keystrokes needed to reach ""?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
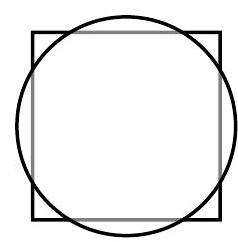
Problem 25: A square with side length and a circle share the same center. The total area of the regions that are inside the circle and outside the square is equal to the total area of the regions that are outside the circle and inside the square. What is the radius of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions