¶ 2021 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2021 AIME II problems here.
Discussion Forum
Engage in discussion about the 2021 AIME II math contest by visiting Random Math AIME II 2021 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2021 AIME II problems, please refer below:
Problem 1: Find the arithmetic mean of all the three-digit palindromes. (Recall that a palindrome is a number that reads the same forward and backward, such as or .)
Solution:
Problem 2: Equilateral triangle has side length . Point lies on the same side of line as such that . The line through parallel to line intersects sides and at points and , respectively. Point lies on such that is between and is isosceles, and the ratio of the area of to the area of is . Find .
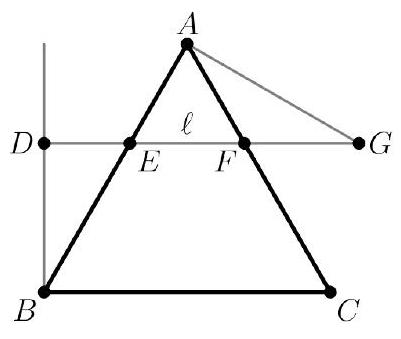
Solution:
Problem 3: Find the number of permutations of numbers such that the sum of five products
is divisible by .
Solution:
Problem 4: There are real numbers , and such that is a root of and is a root of . These two polynomials share a complex root , where and are positive integers and . Find .
Solution:
Problem 5: For positive real numbers , let denote the set of all obtuse triangles that have area and two sides with lengths and . The set of all for which is nonempty, but all triangles in are congruent, is an interval . Find .
Solution:
Problem 6: For any finite set , let denote the number of elements in . Find the number of ordered pairs such that and are (not necessarily distinct) subsets of that satisfy
Solution:
Problem 7: Let , and be real numbers that satisfy the system of equations
There exist relatively prime positive integers and such that
Find .
Solution:
Problem 8: An ant makes a sequence of moves on a cube where a move consists of walking from one vertex to an adjacent vertex along an edge of the cube. Initially the ant is at a vertex of the bottom face of the cube and chooses one of the three adjacent vertices to move to as its first move. For all moves after the first move, the ant does not return to its previous vertex, but chooses to move to one of the other two adjacent vertices. All choices are selected at random so that each of the possible moves is equally likely. The probability that after exactly moves that ant is at a vertex of the top face on the cube is , where and are relatively prime positive integers. Find .
Solution:
Problem 9: Find the number of ordered pairs such that and are positive integers in the set and the greatest common divisor of and is not .
Solution:
Problem 10: Two spheres with radii and one sphere with radius are each externally tangent to the other two spheres and to two different planes and . The intersection of planes and is the line . The distance from line to the point where the sphere with radius is tangent to plane is , where and are relatively prime positive integers. Find .
Solution:
Problem 11: A teacher was leading a class of four perfectly logical students. The teacher chose a set of four integers and gave a different number in to each student. Then the teacher announced to the class that the numbers in were four consecutive two-digit positive integers, that some number in was divisible by , and a different number in was divisible by . The teacher then asked if any of the students could deduce what is, but in unison, all of the students replied no. However, upon hearing that all four students replied no, each student was able to determine the elements of . Find the sum of all possible values of the greatest element of .
Solution:
Problem 12: A convex quadrilateral has area and side lengths , and , in that order. Denote by the measure of the acute angle formed by the diagonals of the quadrilateral. Then can be written in the form , where and are relatively prime positive integers. Find .
Solution:
Problem 13: Find the least positive integer for which is a multiple of .
Solution:
Problem 14: Let be an acute triangle with circumcenter and centroid . Let be the intersection of the line tangent to the circumcircle of at and the line perpendicular to at . Let be the intersection of lines and . Given that the measures of , and are in the ratio , the degree measure of can be written as , where and are relatively prime positive integers. Find .
Solution:
Problem 15: Let and be functions satisfying
and
for positive integers . Find the least positive integer such that .
Solution:
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions