¶ 2022 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2022 AIME I problems here.
Discussion Forum
Engage in discussion about the 2022 AIME I math contest by visiting Random Math AIME I 2022 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2022 AIME I problems, please refer below:
Problem 1: Quadratic polynomials and have leading coefficients and , respectively. The graphs of both polynomials pass through the two points and . Find .
Solution:
Problem 2: Find the three-digit positive integer whose representation in base nine is , where , and are (not necessarily distinct) digits.
Solution:
Problem 3: In isosceles trapezoid , parallel bases and have lengths and , respectively, and . The angle bisectors of and meet at , and the angle bisectors of and meet at . Find .
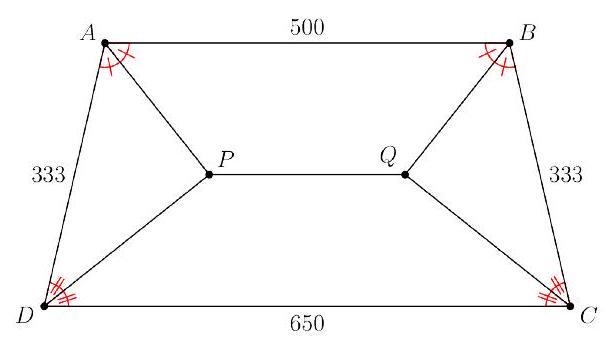
Solution:
Problem 4: Let and , where . Find the number of ordered pairs of positive integers not exceeding that satisfy the equation .
Solution:
Problem 5: A straight river that is meters wide flows from west to east at a rate of meters per minute. Melanie and Sherry sit on the south bank of the river with Melanie a distance of meters downstream from Sherry. Relative to the water, Melanie swims at meters per minute, and Sherry swims at meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find .
Solution:
Problem 6: Find the number of ordered pairs of integers such that the sequence
is strictly increasing and no set of four (not necessarily consecutive) terms forms an arithmetic progression.
Solution:
Problem 7: Let be distinct integers from to . The minimum possible positive value of
can be written as , where and are relatively prime positive integers. Find .
Solution:
Problem 8: Equilateral triangle is inscribed in circle with radius 18. Circle is tangent to sides and and is internally tangent to . Circles and are defined analogously. Circles , and meet in six points-two points for each pair of circles. The three intersection points closest to the vertices of are the vertices of a large equilateral triangle in the interior of , and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of . The side length of the smaller equilateral triangle can be written as , where and are positive integers. Find .
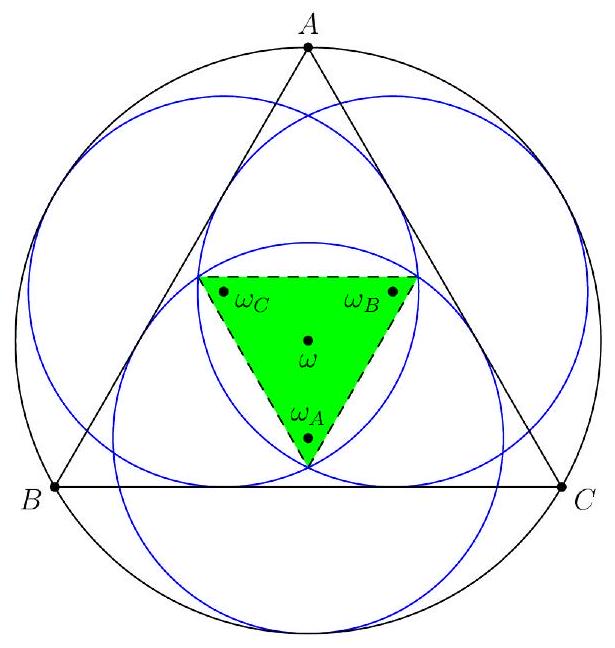
Solution:
Problem 9: Ellina has twelve blocks, two each of red (R), blue (B), yellow (Y), green (G), orange (O), and purple (P). Call an arrangement of blocks even if there is an even number of blocks between each pair of blocks of the same color. For example, the arrangement
is even. Ellina arranges her blocks in a row in random order. The probability that her arrangement is even is , where and are relatively prime positive integers. Find .
Solution:
Problem 10: Three spheres with radii , , and are mutually externally tangent. A plane intersects the spheres in three congruent circles centered at , and , respectively, and the centers of the spheres all lie on the same side of this plane. Suppose that . Find .

Solution:
Problem 11: Let be a parallelogram with . A circle tangent to sides , and intersects diagonal at points and with , as shown. Suppose that , and . Then the area of can be expressed in the form , where and are positive integers, and is not divisible by the square of any prime. Find .
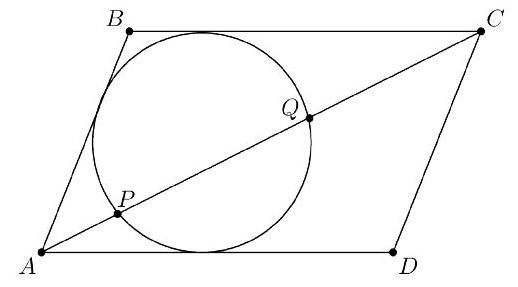
Solution:
Problem 12: For any finite set , let denote the number of elements in . Define
where the sum is taken over all ordered pairs such that and are subsets of with . For example, because the sum is taken over the pairs of subsets
giving . Let , where and are relatively prime positive integers. Find the remainder when is divided by .
Solution:
Problem 13: Let be the set of all rational numbers that can be expressed as a repeating decimal in the form , where at least one of the digits , or is nonzero. Let be the number of distinct numerators obtained when numbers in are written as fractions in lowest terms. For example, both and are counted among the distinct numerators for numbers in because and . Find the remainder when is divided by .
Solution:
Problem 14: Given and a point on one of its sides, call line the splitting line of through if passes through and divides into two polygons of equal perimeter. Let be a triangle where and and are positive integers. Let and be the midpoints of and , respectively, and suppose that the splitting lines of through and intersect at . Find the perimeter of .
Solution:
Problem 15: Let , and be positive real numbers satisfying the system of equations:
Then can be written as , where and are relatively prime positive integers. Find .
Solution:
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions