¶ 2004 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2004 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2004 AMC8 math contest by visiting Random Math 2004 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2004 AMC8 problems, please refer below:
Problem 1: On a map, a -centimeter length represents kilometers. How many kilometers does a -centimeter length represent?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: How many different four-digit numbers can be formed by rearranging the four digits in
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Twelve friends met for dinner at Oscar's Overstuffed Oyster House, and each ordered one meal. The portions were so large, there was enough food for people. If they share, how many meals should they have ordered to have just enough food for the of them?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Ms. Hamilton's eighth-grade class wants to participate in the annual three-person-team basketball tournament.
Lance, Sally, Joy and Fred are chosen for the team. In how many ways can the three starters be chosen?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Ms. Hamilton's eighth-grade class wants to participate in the annual three-person-team basketball tournament.
The losing team of each game is eliminated from the tournament. If sixteen teams compete, how many games will be played to determine the winner?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Ms. Hamilton's eighth-grade class wants to participate in the annual three-person-team basketball tournament.
After Sally takes shots, she has made of her shots. After she takes more shots, she raises her percentage to . How many of the last shots did she make?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: An athlete's target heart rate, in beats per minute, is of the theoretical maximum heart rate. The maximum heart rate is found by subtracting the athlete's age, in years, from . To the nearest whole number, what is the target heart rate of an athlete who is years old?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Find the number of two-digit positive integers whose digits total .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The average of the five numbers in a list is . The average of the first two numbers is . What is the average of the last three numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Handy Aaron helped a neighbor hours on Monday, minutes on Tuesday, from to on Wednesday morning, and a half-hour on Friday. He is paid per hour. How much did he earn for the week?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The numbers and are rearranged according to these rules:
The largest isn't first, but it is in one of the first three places.
The smallest isn't last, but it is in one of the last three places.
The median isn't first or last.
What is the average of the first and last numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Niki usually leaves her cell phone on. If her cell phone is on but she is not actually using it, the battery will last for hours. If she is using it constantly, the battery will last for only hours. Since the last recharge, her phone has been on hours, and during that time she has used it for minutes. If she doesn't talk any more but leaves the phone on, how many more hours will the battery last?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Amy, Bill and Celine are friends with different ages. Exactly one of the following statements is true.
Bill is the oldest.
Amy is not the oldest.
Celine is not the youngest.
Rank the friends from the oldest to the youngest.

Answer Choices:
A. Bill, Amy, Celine
B. Amy, Bill, Celine
C. Celine, Amy, Bill
D. Celine, Bill, Amy
E. Amy, Celine, Bill
Solution:
Problem 14: What is the area enclosed by the geoboard quadrilateral below?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Thirteen black and six white hexagonal tiles were used to create the figure below. If a new figure is created by attaching a border of white tiles with the same size and shape as the others, what will be the difference between the total number of white tiles and the total number of black tiles in the new figure?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Two pitchers contain orange juice. One pitcher is full and the other pitcher is full. Water is added to fill each pitcher completely, then both pitchers are poured into one large container. What fraction of the mixture in the large container is orange juice?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Three friends have a total of identical pencils, and each one has at least one pencil. In how many ways can this happen?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Five friends compete in a dart-throwing contest. Each one has two darts to throw at the same circular target, and each individual's score is the sum of the scores in the target regions that are hit. The scores for the target regions are the whole numbers through . Each throw hits the target in a region with a different value. The scores are: Alice points, Ben points, Cindy points, Dave points, and Ellen points. Who hits the region worth points?
.jpg)
Answer Choices:
A. Alice
B. Ben
C. Cindy
D. Dave
E. Ellen
Solution:
Problem 19: A whole number larger than leaves a remainder of when divided by each of the numbers and . The smallest such number lies between which two numbers?
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 20: Two-thirds of the people in a room are seated in three-fourths of the chairs. The rest of the people are standing. If there are empty chairs, how many people are in the room?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Spinners and are spun. On each spinner, the arrow is equally likely to land on each number. What is the probability that the product of the two spinners' numbers is even?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: At a party there are only single women and married men with their wives. The probability that a randomly selected woman is single is . What fraction of the people in the room are married men?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
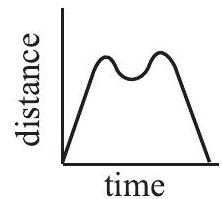
Problem 23: Tess runs counterclockwise around rectangular block . She lives at corner . Which graph could represent her straight-line distance from home?
.jpg)
Answer Choices:
A.
.jpg)
.jpg)
.jpg)
.jpg)
Solution:
Problem 24: In the figure, is a rectangle and is a parallelogram. Using the measurements given in the figure, what is the length of the segment that is perpendicular to and
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
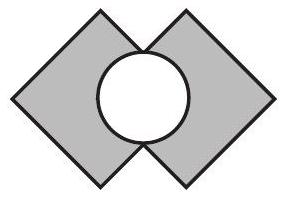
Problem 25: Two squares intersect at right angles, bisecting their intersecting sides, as shown. The circle's diameter is the segment between the two points of intersection. What is the area of the shaded region created by removing the circle from the squares?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions