¶ 2013 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2013 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2013 AMC8 math contest by visiting Random Math 2013 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2013 AMC8 problems, please refer below:
Problem 1: Danica wants to arrange her model cars in rows with exactly cars in each row. She now has model cars. What is the smallest number of additional cars she must buy in order to be able to arrange her cars in this way?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A sign at the fish market says, " off, today only: half-pound packages for just per package." What is the regular price for a full pound of fish, in dollars?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra to cover her portion of the total bill. What was the total bill?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Hammie is in the grade and weighs pounds. His quadruplet sisters are tiny babies and weigh , and pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?
Answer Choices:
A. median, by
B. median, by
C. average, by
D. average, by
E. average, by
Solution:
Problem 6: The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted cars in the first seconds. It took the train minutes and seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A fair coin is tossed times. What is the probability of at least two consecutive heads?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is meter, the second jump is meters, the third jump is meters, and so on, then on which jump will he first be able to jump more than kilometer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: What is the ratio of the least common multiple of and to the greatest common factor of and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Ted's grandfather used his treadmill on days this week. He went miles each day. On Monday he jogged at a speed of miles per hour. He walked at the rate of miles per hour on Wednesday and at miles per hour on Friday. If Grandfather had always walked at miles per hour, he would have spent less time on the treadmill. How many minutes less?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: At the Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of , you get a second pair at a discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the regular price did he save?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Abe holds green and red jelly bean in his hand. Bea holds green, yellow, and red jelly beans in her hand. Each randomly picks a jelly bean to show the other. What is the probability that the colors match?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If , and , what is the product of , and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The sum of six consecutive positive integers is . What is the largest of these six integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Isabella uses one-foot cubical blocks to build a rectangular fort that is feet long, feet wide, and feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?
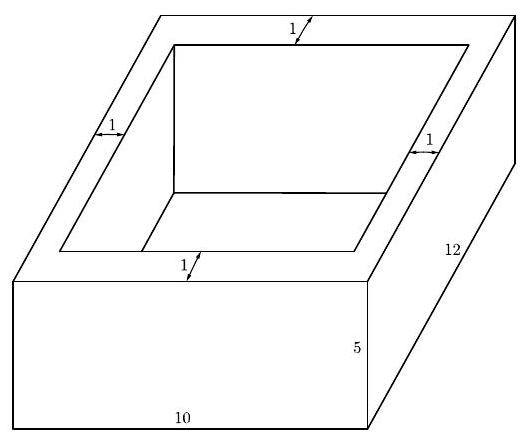
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show their tests to anyone. Cassie says, "I didn't get the lowest score in our class," and Bridget adds, "I didn't get the highest score." What is the ranking of the three girls from highest to lowest?
Answer Choices:
A. Hannah, Cassie, Bridget
B. Hannah, Bridget, Cassie
C. Cassie, Bridget, Hannah
D. Cassie, Hannah, Bridget
E. Bridget, Cassie, Hannah
Solution:
Problem 20: A rectangle is inscribed in a semicircle with the longer side on the diameter. What is the area of the semicircle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Samantha lives blocks west and block south of the southwest corner of City Park. Her school is blocks east and blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner of City Park, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Toothpicks are used to make a grid that is toothpicks long and toothpicks high. How many toothpicks are used altogether?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length . What is the radius of the semicircle on
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Squares , and are equal in area. Points and are the midpoints of sides and , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?
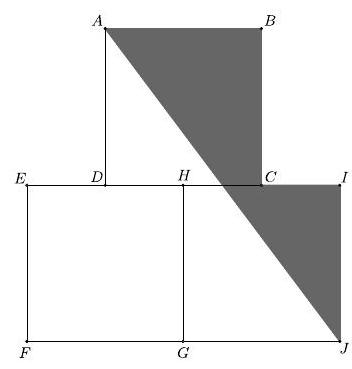
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A ball with diameter inches starts at point to roll along the track shown. The track is comprised of semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance in inches the center of the ball travels over the course from to
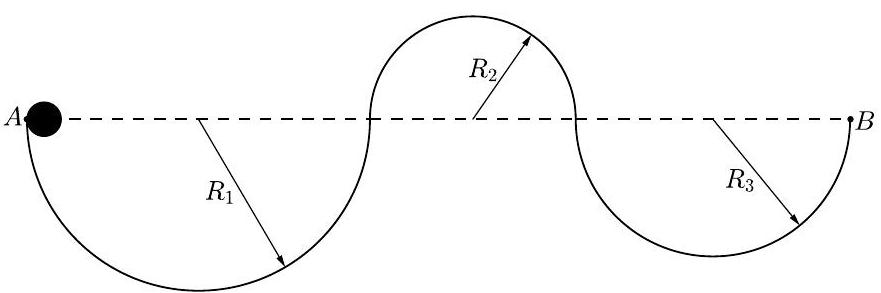
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions