¶ 1956 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1956 AHSME problems, please refer below:
Problem 1: The value of when is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Mr. Jones sold two pipes at each. Based on the cost his profit on one was and his loss on the other was . On the sale of the pipes, he
Answer Choices:
A. broke even
B. lost cents
C. gained cents
D. lost cents
E. gained cents
Solution:
Problem 3: The distance light travels in one year is approximately miles. The distance light travels in 100 years is:
Answer Choices:
A. miles
B. miles
C. miles
D.
E.
Solution:
Problem 4: A man has to invest. He invests at and at . In order to have a yearly income of , he must invest the remainder at:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A nickel is placed on a table. The number of nickels which can be placed around it, each tangent to it and to two others is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: In a group of cows and chickens, the number of legs was 14 more than twice the number of heads. The number of cows was:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The roots of the equation will be reciprocal if:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: If , then, when
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Simplify:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A circle of radius 10 inches has its center at the vertex of an equilateral triangle and passes through the other two vertices. The side extended through intersects the circle at . The number of degrees of angle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The expression equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If is divided by the quotient is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The percent that is less than is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The points , and are on a circle 0 . The tangent line at and the secant intersect at . If and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The roots of are
Answer Choices:
A. -5 and 3
B.
C. only 2
D. -3 and 5
E. only 3
Solution:
Problem 16: The sum of three numbers is 98. The ratio of the first to the second is , and the ratio of the second to the third is . The second number is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The fraction was obtained by adding the two fractions and . The values of and must be:
Answer Choices:
A. ,
B. ,
C. ,
D. ,
E. ,
Solution:
Problem 18: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Two candles of the same height are lighted at the same time. The first is consumed in 4 hours and the second in 3 hours. Assuming that each candle burns at a constant rate, in how many hours after being lighted was the first candle twice the height of the second?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If and , then the value of to the nearest tenth is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If each of two intersecting lines intersects a hyperbola and neither line is tangent to the hyperbola, then the possible number of points of intersection with the hyperbola is:
Answer Choices:
A.
B. or
C. or
D. or
E. or
Solution:
Problem 22: Jones covered a distance of miles on his first trip. On a later trip he traveled miles while going three times as fast. His new time compared with the old time was:
Answer Choices:
A. three times as long
B. twice as long
C. the same
D. half as long
E. a third as long
Solution:
Problem 23: For the equation we have . A description of the roots is that they are:
Answer Choices:
A. equal and rational
B. unequal and rational
C. equal and irrational
D. unequal and irrational
E. equal and imaginary
Solution:
Problem 24: In the figure , angle , and .
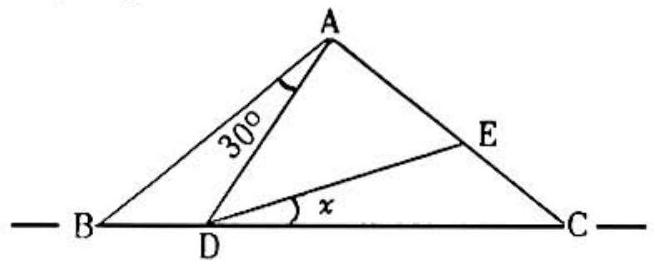
Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The sum of all numbers of the form , where takes on integral values from 1 to is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Which one of the following combinations of given parts does not determine the indicated triangle?
Answer Choices:
A. base angle and vertex angle; isosceles triangle
B. vertex angle and the base; isosceles triangle
C. the radius of the circumscribed circle; equilateral triangle
D. one arm and the radius of the inscribed circle; right triangle
E. two angles and a side opposite one of them; scalene triangle
Solution:
Problem 27: If an angle of a triangle remains unchanged but each of its two including sides is doubled, then the area is multiplied by:
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 28: Mr. J left his entire estate to his wife, his daughter, his son, and the cook. His daughter and son got half the estate, sharing in the ratio of 4 to 3. His wife got twice as much as the son. If the cook received a bequest of , then the entire estate was:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: The points of intersection of and are joined. The resulting figure is:
Answer Choices:
A. a straight line
B. an equilateral triangle
C. a parallelogram
D. a rectangle
E. a square
Solution:
Problem 30: If the altitude of an equilateral triangle is , then the area is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: In our number system the base is ten. If the base were changed to four you would count as follows: The twentieth number would be:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: George and Henry started a race from opposite ends of the pool. After a minute and a half, they passed each other in the center of the pool. If they lost no time in turning and maintained their respective speeds, how many minutes after starting did they pass each other the second time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: The number is equal to:
Answer Choices:
A. a rational fraction
B. a finite decimal
C.
D. an infinite repeating decimal
E. an infinite non-repeating decimal
Solution:
Problem 34: If is any whole number, is always divisible by:
Answer Choices:
A.
B.
C. Any multitude of
D.
E. and
Solution:
Problem 35: A rhombus is formed by two radii and two chords of a circle whose radius is 15 feet. The area of the rhombus in square feet is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 36: If the sum is a perfect square and if is less than 100 , then the possible values for are:
Answer Choices:
A. only 1
B. 1 and 8
C. only 8
D. 8 and 49
E. 1,8 , and 49
Solution:
Problem 37: On a map whose scale is 400 miles to an inch and a half, a certain estate is represented by a rhombus having a angle. The diagonal opposite is . The area of the estate in square miles is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: In a right triangle with sides and , and hypotenuse , the altitude drawn on the hypotenuse is . Then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 39: The hypotenuse and one arm of a right triangle are consecutive integers. The square of the second arm is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 40: If and then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 41: The equation where is satisfied by:
Answer Choices:
A. no value of
B. all values of
C. only
D. all integral values of only
E. all rational values of only
Solution:
Problem 42: The equation has:
Answer Choices:
A. no root
B. one real root
C. one real root and one imaginary root
D. two imaginary roots
E. two real roots
Solution:
Problem 43: The number of scalene triangles having all sides of integral lengths, and perimeter less than 13 is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 44: If means that and are numbers such that is less than and is less than zero, then
Answer Choices:
A.
B.
C.
D. but
E. but
Solution:
Problem 45: A wheel with a rubber tire has an outside diameter of 25 in . When the radius has been decreased a quarter of an inch, the number of revolutions of the wheel in one mile will:
Answer Choices:
A. be increased about
B. be increased about
C. be increased about 20%
D. be increased by
E. remain the same
Solution:
Problem 46: In the equation where is positive, can have:
Answer Choices:
A. any positive value less than 1
B. any value less than 1
C. the value zero only
D. any non-negative value
E. any value
Solution:
Problem 47: An engineer said he could finish a highway section in 3 days with his present supply of a certain type of machine. However, with 3 more of these machines the jab could be done in 2 days. If the machines all work at the same rate, how many days would it take to do the job with one machine?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 48: If is a positive integer, then can be a positive integer, if and only if is:
Answer Choices:
A. at least 3
B. at least 3 and no more than 35
C. no more than 35
D. equal to 35
E. equal to 3 or 35
Solution:
Problem 49: Triangle is formed by three tangents to circle . Angle , then angle equals:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 50: In triangle . On square is constructed away from the triangle. If is the number of degrees in angle , then
Answer Choices:
A. depends upon triangle
B. is independent of the triangle
C. may equal angle
D. can never equal angle
E. is greater than but less than
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions