¶ 1957 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1957 AHSME problems, please refer below:
Problem 1: The number of distinct lines representing the altitudes, medians, and interior angle bisectors of a triangle that is isosceles, but not equilateral, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: In the equation , the sum of the roots is 4 and the product of the roots is -3 . Then and have the values, respectively:
Answer Choices:
A. 8 and -6
B. 4 and -3
C. -3 and 4
D. -3 and 8
E. 8 and -3
Solution:
Problem 3: The simplest form of is:
Answer Choices:
A. a if
B.
C. a if
D. 1 - a with no restriction on a
E. if
Solution:
Problem 4: The first step in finding the product by use of the distributive property in the form is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Through the use of theorems of can be reduced to:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: An open box is constructed by starting with a rectangular sheet of metal 10 in . by 14 in . and cutting a square of side x inches from each corner. The resulting projections are folded up and the seams welded. The volume of the resulting box is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 7: The area of a circle inscribed in an equilateral triangle is . The perimeter of this triangle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The numbers are proportional to . The sum of , and is 100 . The number is given by the equation . Then a is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The value of when and is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The graph of has its:
Answer Choices:
A. lowest point at
B. lowest point at
C. lowest point at
D. highest point at
E. highest point at
Solution:
Problem 11: The angle formed by the hands of a clock at is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 12: Comparing the numbers and we may say:
Answer Choices:
A. the first exceeds the second by
B. the first exceeds the second by
C. the first exceeds the second by
D. the second is five times the first
E. the first exceeds the second by 5
Solution:
Problem 13: A rational number between and is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: If , then is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 15: The table below shows the distance in feet a ball rolls down an inclined plane in seconds.
The distance for is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Goldfish are sold at cents each. The rectangular coordinate graph showing the cost of 1 to 12 goldfish is:
Answer Choices:
A. a straight line segment
B. a set of horizontal parallel line segments
C. a set of vertical parallel line segments
D. a finite set of distinct points
E. a straight line
Solution:
Problem 17: A cube is made by soldering twelve 3 -inch lengths of wire properly at the vertices of the cube. If a fly alights at one of the vertices and then walks along the edges, the greatest distance it could travel before coming to any vertex a second time, without retracing any distance, is:
Answer Choices:
A. 24 in
B. 12 in
C. 30 in
D. 18 in
E. 36 in
Solution:
Problem 18: Circle has diameters and perpendicular to each other. is any chord intersecting at . Then is equal to:
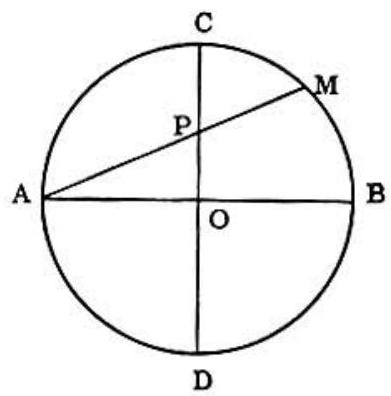
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The base of the decimal number system is ten, meaning, for example, that . In the binary system, which has base two, the first five positive integers are 1, 10, 11, 100, 101. The numeral 10011 in the binary system would then be written in the decimal system as:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A man makes a trip by automobile at an average speed of mph . He returns over the same route at an average speed of mph . His average speed for the entire trip is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 21: Start with the theorem "If two angles of a triangle are equal, the triangle is isosceles" and the following four statements
- If two angles of a triangle are not equal, the triangle is not isosceles
- The base angles of an isosceles triangle are equal
- If a triangle is not isosceles, then two of its angles are not equal
- A necessary condition that two angles of a triangle be equal is that the triangle be isosceles.
Which combination of statements contains only those which follow logically from the given theorem or which have the same verbal meaning as the given theorem?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: If , then equals:
Answer Choices:
A.
B.
C.
D.
E. no real value
Solution:
Problem 23: The graph of and the graph of meet in two points. The distance between these two points is:
Answer Choices:
A. less than 1
B.
C.
D.
E. more than 2
Solution:
Problem 24: If the square of a number of two digits is decreased by the square of the number formed by reversing the digits, then the result is not always divisible by:
Answer Choices:
A.
B. the product of the digits
C. the sum of the digits
D. the difference of the digits
E.
Solution:
Problem 25: The vertices of triangle have coordinates as follows: , , where and are positive. The area of triangle may be found from the expression:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: From a point within a triangle, line segments are drawn to the vertices. A necessary and sufficient condition that the three triangles thus formed have equal areas is that the point be:
Answer Choices:
A. the center of the inscribed circle
B. the center of the circumscribed circle
C. such that the three angles formed at the point each be
D. the intersection of the altitudes of the triangle
E. the intersection of the medians of the triangle
Solution:
Problem 27: The sum of the reciprocals of the roots of the equation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: If and are positive and , then the value of is:
Answer Choices:
A. dependent upon
B. dependent upon a
C. dependent upon and
D. zero
E. one
Solution:
Problem 29: The relation is true for:
Where a means that can take on all values greater than a and the value equal to a, while has a corresponding meaning with "less than."
Answer Choices:
A. only
B.
C.
D.
E. only
Solution:
Problem 30: The sum of the squares of the first positive integers is given by the expression , if c and k are, respectively:
Answer Choices:
A. 1 and 2
B. 3 and 5
C. 2 and 2
D. 1 and 1
E. 2 and 1
Solution:
Problem 31: A regular octagon is to be formed by cutting equal isosceles right triangles from the corners of a square. If the square has sides of one unit, the leg of each of the triangles is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: The largest of the following integers which divides each of the members of the sequence is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: If , then the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: The points that satisfy the system , where the symbol "<" means "less than," are:
Answer Choices:
A. only two points
B. an arc of a circle
C. a straight line segment not including the end-points
D. a straight line segment including the end-points
E. a single point
Solution:
Problem 35: Side of right triangle is divided into 8 equal parts. Seven line segments parallel to are drawn to from the points of division. If , then the sum of the lengths of the seven line segments:
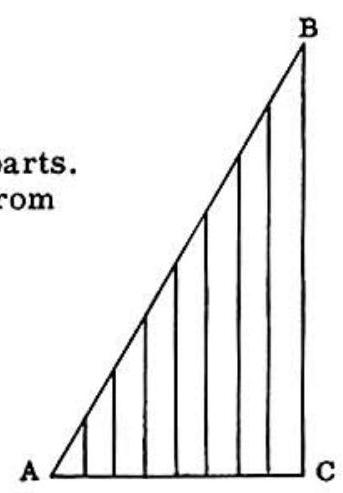
Answer Choices:
A. can not be found from the given information
B. is 33
C. is 34
D. is 35
E. is 45
Solution:
Problem 36: If , then the largest value of is:
Answer Choices:
A.
B.
C. an irrational number about 0.4
D.
E.
Solution:
Problem 37: In right triangle , and ; is on . If , onehalf the perimeter of rectangle , then:
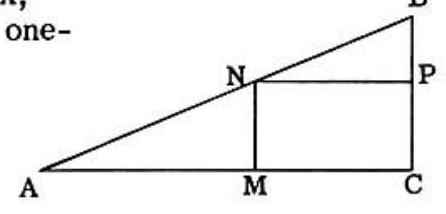
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: From a two-digit number N we subtract the number with the digits reversed and find that the result is a positive perfect cube. Then:
Answer Choices:
A. N cannot end in 5
B. N can end in any digit other than 5
C. N does not exist
D. there are exactly 7 values for N
E. there are exactly 10 values for N
Solution:
Problem 39: Two men set out at the same time to walk towards each other from M and N , miles apart. The first man walks at the rate of 4 mph . The second man walks miles the first hour, miles the second hour, miles the third hour, and so on in arithmetic progression. Then the men will meet:
Answer Choices:
A. in hours
B. in hours
C. nearer than
D. nearer than
E. midway between and
Solution:
Problem 40: If the parabola has its vertex on the -axis, then must be:
Answer Choices:
A. a positive integer
B. a positive or a negative rational number
C. a positive rational number
D. a positive or a negative irrational number
E. a negative irrational number
Solution:
Problem 41: Given the system of equations . For which one of the following values of is there no solution for and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 42: If , where and n is an integer, then the total number of possible distinct values for is:
Answer Choices:
A.
B.
C.
D.
E. more than 4
Solution:
Problem 43: We define a lattice point as a point whose coordinates are integers, zero admitted. Then the number of lattice points on the boundary and inside the region bounded by the -axis, the line , and the parabola is:
Answer Choices:
A.
B.
C.
D.
E. not finite
Solution:
Problem 44: In triangle and . Then is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 45: If two real numbers and satisfy the equation , then:
Answer Choices:
A. and where a means that can take any value greater than a or equal to a
B. can equal 1
C. both x and y must be irrational
D. x and y cannot both be integers
E. both x and y must be rational
Solution:
Problem 46: Two perpendicular chords intersect in a circle. The segments of one chord are 3 and 4 ; the segments of the other are 6 and 2 . Then the diameter of the circle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 47: In circle , the midpoint of radius is ; at , . The semi-circle on AB as diameter intersects in . Line AM intersects circle in , and line BM intersects circle in . Line is drawn. Then, if the radius of circle is is:
.jpg)
Answer Choices:
A.
B.
C. not a side of an inscribed regular polygon
D.
E.
Solution:
Problem 48: Let ABC be an equilateral triangle inscribed in circle . is a point on arc BC. Lines AM, , and are drawn. Then is:
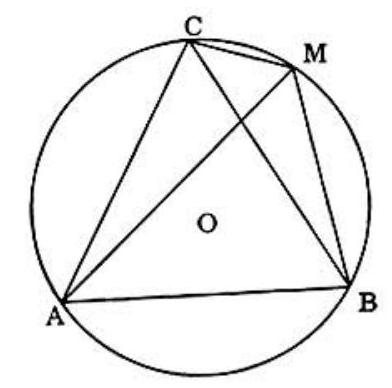
Answer Choices:
A. equal to
B. less than
C. greater than
D. equal, less than, or greater than , depending upon the position of
E. none of these
Solution:
Problem 49: The parallel sides of a trapezoid are 3 and 9. The non-parallel sides are 4 and 6. A line parallel to the bases divides the trapezoid into two trapezoids having equal perimeters. The ratio into which each of the non-parallel sides is divided is:
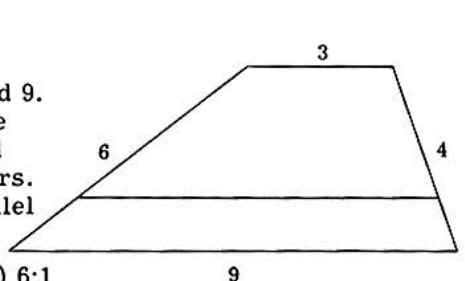
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 50: In circle is a moving point on diameter . is drawn perpendicular to AB and equal to is drawn perpendicular to AB , on the same side of diameter as , and equal to . Let be the midpoint of . Then, as moves from to , point :
Answer Choices:
A. moves on a straight line parallel to
B. remains stationary
C. moves on a straight line perpendicular to AB
D. moves in a small circle intersecting the given circle
E. follows a path which is neither a circle nor a straight line
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions