¶ 1958 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1958 AHSME problems, please refer below:
Problem 1: The value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Of the following expressions the one equal to is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: In the expression each is replaced by . The resulting expression, evaluated for , equals:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 5: The expression equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The arithmetic mean between and , when , is (the symbol means "not equal to"):
Answer Choices:
A. 2 , if a
B.
C. 1 , if only
D.
E.
Solution:
Problem 7: A straight line joins the points and . Its -intercept is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Which of these four numbers , is (are) rational;
Answer Choices:
A.
B.
C. the first and fourth
D. only the fourth
E. only the first
Solution:
Problem 9: A value of satisfying the equation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: For what real values of , other than , does the equation have real roots? (The symbol a means that can take on all values greater than a and the value a itself; a has the corresponding meaning with "less than".)
Answer Choices:
A.
B.
C.
D. all values of
E. no values of
Solution:
Problem 11: The number of roots satisfying the equation is:
Answer Choices:
A. unlimited
B.
C.
D.
E.
Solution:
Problem 12: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The sum of two numbers is 10 ; their product is 20 . The sum of their reciprocals is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: At a dance party a group of boys and girls exchange dances as follows: one boy dances with 5 girls, a second boy dances with 6 girls, and so on, the last boy dancing with all the girls. If b represents the number of boys and g , the number of girls, then:
Answer Choices:
A.
B.
C.
D.
E. It is impossible to determine a relation between and without knowing the total number of boys and girls.
Solution:
Problem 15: A quadrilateral is inscribed in a circle. If an angle is inscribed into each of the four segments outside the quadrilateral, the sum of these four angles, expressed in degrees, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The area of a circle inscribed in a regular hexagon is . The area of the hexagon is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If is positive and , then:
Answer Choices:
A. has no minimum or maximum value
B. the maximum value of x is 1
C. the minimum value of is 1
D. the maximum value of is 4
E. the minimum value of is 4
Solution:
Problem 18: The area of a circle is doubled when its radius is increased by . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The sides of a right triangle are and and the hypotenuse is . A perpendicular from the vertex divides c into segments r and s , adjacent respectively to a and b . If , then the ratio of to is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: In the accompanying figure CE and DE are equal chords of a circle with center . Arc AB is a quarter-circle. Then the ratio of the area of triangle CED to the area of triangle is:
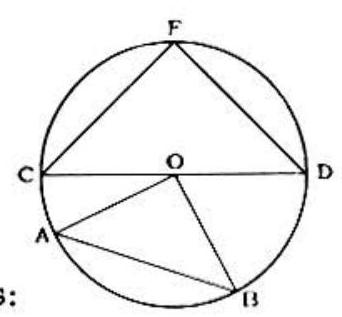
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A particle is placed on the parabola at a point whose ordinate is 6. It is allowed to roll along the parabola until it reaches the nearest point whose ordinate is -6 . The horizontal distance traveled by the particle (the numerical value of the difference in the abscissas of and ) is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If, in the expression , increases or decreases by a positive amount , the expression changes by an amount:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A man travels feet due north at 2 minutes per mile. He returns due south to his starting point at 2 miles per minute. The average rate in miles per hour for the entire trip is:
Answer Choices:
A.
B.
C.
D.
E. impossible to determine without knowing the value of
Solution:
Problem 25: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: A set of numbers has the sum . Each number of the set is increased by 20 , then multiplied by 5 , and then decreased by 20 . The sum of the numbers in the new set thus obtained is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: The points and are on the same straight line. The value(s) of is (are):
Answer Choices:
A.
B.
C.
D. 12 or 6
E. 6 or
Solution:
Problem 28: A 16 -quart radiator is filled with water. Four quarts are removed and replaced with pure antifreeze liquid. Then four quarts of the mixture are removed and replaced with pure antifreeze. This is done a third and a fourth time. The fractional part of the final mixture that is water is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: In a general triangle ADE (as shown in the diagram) lines EB and EC are drawn. Which of the following angle relations is true?
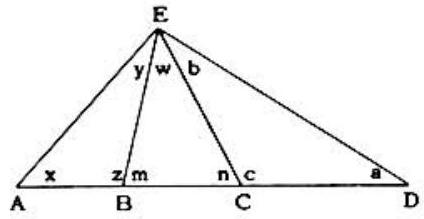
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: If and , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: The altitude drawn to the base of an isosceles triangle is 8 , and the perimeter is 32 . The area of the triangle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: With a rancher is to buy steers at each and cows at each. If the number of steers and the number of cows are both positive integers, then:
Answer Choices:
A. this problem has no solution
B. there are two solutions with s exceeding c
C. there are two solutions with exceeding
D. there is one solution with exceeding
E. there is one solution with exceeding
Solution:
Problem 33: For one root of to be double the other, the coefficients must be related as follows:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: The numerator of a fraction is , the denominator is , and can have any value between -2 and 2 , both included. The values of for which the numerator is greater than the denominator are:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: A triangle is formed by joining three points whose coordinates are integers. If the -unit and the -unit are each 1 inch, then the area of the triangle, in square inches, must be an integer
Answer Choices:
A. must be an integer
B. may be irrational
C. must be irrational
D. must be rational
E. will be an integer only if the triangle is equilateral.
Solution:
Problem 36: The sides of a triangle are 30,70 , and 80 units. If an altitude is dropped upon the side 80 , the larger segment cut off on this side is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 37: The first term of an arithmetic series of consecutive integers is . The sum of terms of this series may be expressed as:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: Let be the distance from the origin to a point with coordinates and . Designate the ratio by and the ratio by . Then the values of are limited to the numbers:
Answer Choices:
A. less than -1 and greater than +1 , both excluded
B. less than -1 and greater than +1 , both included
C. between -1 and +1 , both excluded
D. between -1 and +1 , both included
E. -1 and +1 only
Solution:
Problem 39: The symbol means if is not negative and if is not positive. We may then say concerning the solution of that:
Answer Choices:
A. there is only one root
B. the sum of the roots is +1
C. the sum of the roots is 0
D. the product of the roots is +4
E. the product of the roots is -6
Solution:
Problem 40: Given , and the general relation for . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 41: The roots of are and . For the roots of to be and must equal:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 42: In a circle with center chord chord . Chord cuts in . If and , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 43: AB is the hypotenuse of a right triangle ABC . Median and median . The length of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 44: Given the true statements: (1) If a is greater than , then is greater than (2) If is less than , then is greater than . A valid conclusion is:
Answer Choices:
A. If a is less than , then is greater than
B. If is greater than , then a is less than
C. If is less than , then is greater than
D. If is greater than , then is less than
E. none of these
Solution:
Problem 45: A check is written for dollars and cents, and both two-digit numbers. In error it is cashed for dollars and cents, the incorrect amount exceeding the correct amount by . Then:
Answer Choices:
A. cannot exceed 70
B. can equal
C. the amount of the check cannot be a multiple of 5
D. the incorrect amount can equal twice the correct amount
E. the sum of the digits of the correct amount is divisible by 9
Solution:
Problem 46: For values of less than 1 but greater than -4 , the expression has:
Answer Choices:
A. no maximum or minimum value
B. a minimum value of +1
C. a maximum value of +1
D. a minimum value of -1
E. a maximum value of -1
Solution:
Problem 47: is a rectangle (see the accompanying diagram) with any point on . and . and . Then is equal to:
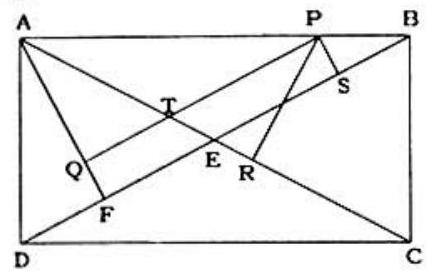
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 48: Diameter AB of a circle with center 0 is 10 units. C is a point 4 units from A , and on AB . D is a point 4 units from B , and on AB . P is any point on the circle. Then the broken-line path from to to :
Answer Choices:
A. has the same value for all positions of
B. exceeds 10 units for all positions of
C. cannot exceed 10 units
D. is the least when CPD is a right triangle
E. is the greatest when is equidistant from and
Solution:
Problem 49: In the expansion of there are dissimilar terms. The number of dissimilar terms in the expansion of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 50: In this diagram a scheme is indicated for associating all the points of segment with those of segment , and reciprocally. To describe this association scheme analytically let be the distance from a point on to D and let y be the distance from the associated point of to . Then for any pair of associated points, if equals:
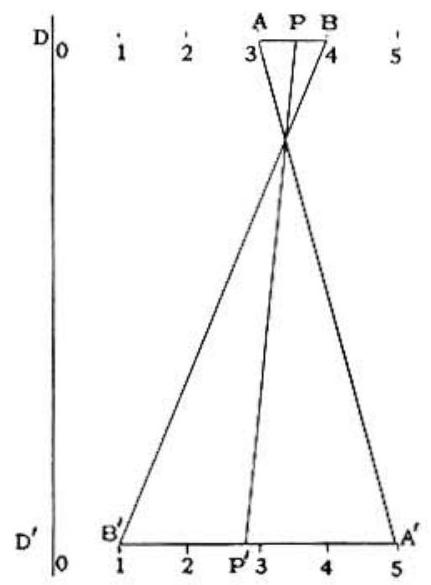
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions