¶ 1960 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1960 AHSME problems, please refer below:
Problem 1: If 2 is a solution (root) of , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: It takes 5 seconds for a clock to strike 6 o'clock beginning at 6:00 o'clock precisely. If the strikings are uniformly spaced, how long, in seconds, does it take to strike 12 o'clock?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 3: Applied to a bill for the difference between a discount of and two successive discounts of and , expressed in dollars, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Each of two angles of a triangle is and the included side is 4 inches. The area of the triangle, in square inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The number of distinct points common to the graphs of and is:
Answer Choices:
A. infinitely many
B. four
C. two
D. one
E. none
Solution:
Problem 6: The circumference of a circle is 100 inches. The side of a square inscribed in this circle, expressed in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Circle I passes through the center of, and is tangent to, circle II. The area of circle is 4 square inches. Then the area of circle II, in square inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The number can be written as a fraction. When reduced to lowest terms the sum of the numerator and denominator of this fraction is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 9: The fraction is (with suitable restrictions on the values of , and ):
Answer Choices:
A. irreducible
B. reducible to -1
C. reducible to a polynomial of three terms
D. reducible to
E. reducible to
Solution:
Problem 10: Given the following six statements:
(1) All women are good drivers
(2) Some women are good drivers
(3) No men are good drivers
(4) All men are bad drivers
(5) At least one man is a bad driver
(6) All men are good drivers.
The statement that negates statement (6) is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: For a given value of the product of the roots of is 7 . The roots may be characterized as:
Answer Choices:
A. integral and positive
B. integral and negative
C. rational, but not integral
D. irrational
E. imaginary
Solution:
Problem 12: The locus of the centers of all circles of given radius a, in the same plane, passing through a fixed point, is:
Answer Choices:
A. a point
B. a straight line
C. two straight lines
D. a circle
E. two circles
Solution:
Problem 13: The polygon(s) formed by , and , is (are):
Answer Choices:
A. an equilateral triangle
B. an isosceles triangle
C. a right triangle
D. a triangle and a trapezoid
E. a quadrilateral
Solution:
Problem 14: If and are real numbers, the equation has a unique solution [the symbol a means that a is different from zero]:
Answer Choices:
A. for all and
B. if a
C. if
D. if
E. if
Solution:
Problem 15: Triangle is equilateral with side , perimeter , area , and circumradius (radius of the circumscribed circle). Triangle II is equilateral with side , perimeter , area , and circumradius . If is different from , then:
Answer Choices:
A. only sometimes
B. P:p = R:r always
C. P:p = K:k only sometimes
D. always
E. R:r = K:k only sometimes
Solution:
Problem 16: In the numeration system with base 5 , counting is as follows: , The number whose description in the decimal system is 69 , when described in the base 5 system, is a number with:
Answer Choices:
A. two consecutive digits
B. two non-consecutive digits
C. three consecutive digits
D. three non-consecutive digits
E. four digits
Solution:
Problem 17: The formula gives, for a certain group, the number of individuals whose income exceeds dollars. The lowest income, in dollars, of the wealthiest 800 individuals is at least:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The pair of equations and has:
Answer Choices:
A. no common solution
B. the solution
C. the solution
D. a common solution in positive and negative integers
E. none of these
Solution:
Problem 19: Consider equation : where , and are positive integers, and equation II: , where , and are positive integers. Then:
Answer Choices:
A. I can be solved in consecutive integers
B. I can be solved in consecutive even integers
C. II can be solved in consecutive integers
D. II can be solved in consecutive even integers
E. II can be solved in consecutive odd integers
Solution:
Problem 20: The coefficient of in the expansion of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The diagonal of square is . The perimeter of square II with twice the area of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The equality , where and are unequal nonzero constants, is satisfied by where:
Answer Choices:
A. has a unique non-zero value
B. has two non-zero values
C. , has a unique non-zero value
D. , has two non-zero values
E. and each have a unique non-zero value.
Solution:
Problem 23: The radius of a cylindrical box is 8 inches, the height , is 3 inches. The volume is to be increased by the same fixed positive amount when is increased by inches as when is increased by inches. This condition is satisfied by:
Answer Choices:
A. no real value of
B. one integral value of
C. one rational, but not integral, value of
D. one irrational value of
E. two real values of
Solution:
Problem 24: If , where is real, then is:
Answer Choices:
A. A non-square, non-cube integer
B. a non-square, non-cube, nonintegral rational number
C. an irrational number
D. a perfect square
E. a perfect cube
Solution:
Problem 25: Let and be any two odd numbers, with less than . The largest integer which divides all possible numbers of the form is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Find the set of -values satisfying the inequality . [The symbol means if a is positive, if is negative, 0 if a is zero. The notation means that a can have any value between 1 and 2 , excluding 1 and 2.]
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Let be the sum of the interior angles of a polygon for which each interior angle is times the exterior angle at the same vertex. Then
Answer Choices:
A. and P may be regular
B. and P is not regular
C. and P is regular
D. and is not regular
E. and P may or may not be regular
Solution:
Problem 28: The equation has:
Answer Choices:
A. infinitely many integral roots
B. no root
C. one integral root
D. two equal integral roots
E. two equal non-integral roots
Solution:
Problem 29: Five times A's money added to B's money is more than . Three times A's money minus B's money is . If a represents 's money in dollars and represents 's money in dollars, then:
Answer Choices:
A. a , b
B. a , b
C.
D. a , but we can put no bounds on
E.
Solution:
Problem 30: Given the line and a point on this line equidistant from the coordinate axes. Such a point exists in:
Answer Choices:
A. none of the quadrants
B. quadrant I only
C. quadrants I, II only
D. quadrants I, II, III only
E. each of the quadrants
Solution:
Problem 31: For to be a factor of , the values of and must be, respectively:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: In this figure the center of the circle is . , is a straight line, , and has a length twice the radius. Then:
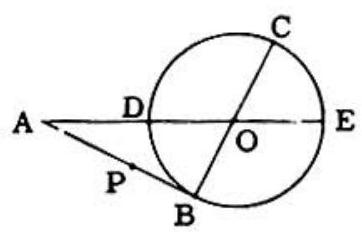
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 33: You are given a sequence of 58 terms, each of which is of the form , where the first term is the product of all prime numbers (a prime number is one divisible only by 1 and itself) beginning with 2 and ending with 61, and the second term is one of the natural numbers, taken in order, beginning with 2 and ending with 59 , inclusive. Let N be the number of primes appearing in this sequence. Then is:
Answer Choices:
A. zero
B. sixteen
C. seventeen
D. fifty-seven
E. fifty-eight
Solution:
Problem 34: Two swimmers, at opposite ends of a 90 -foot pool, start to swim the length of the pool, one at the rate of 3 feet per second, the other at 2 feet per second. They swim back and forth for 12 minutes. Allowing no loss of time at the turns, find the number of times they pass each other.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: From point outside a circle, with a circumference of 10 units, a tangent is drawn. Also from P a secant is drawn dividing the circle into unequal arcs with lengths and . It is found that , the length of the tangent, is the mean proportional between and . If and are integers, then may have the following number of values:
Answer Choices:
A. zero
B. one
C. two
D. three
E. infinitely many
Solution:
Problem 36: Let be the respective sums of terms of the same arithmetic progression with a as the first term and as the common difference. Let . Then is dependent on:
Answer Choices:
A. and d
B. and
C. and
D. , and
E. neither a nor nor
Solution:
Problem 37: The base of a triangle is of length , and the altitude is of length . A rectangle of height is inscribed in the triangle with the base of the rectangle in the base of the triangle. The area of the rectangle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: In this diagram and are the equal sides of an isosceles triangle , in which is inscribed equilateral triangle DEF. Designate angle BFD by a, angle ADE by , and angle FEC by . Then
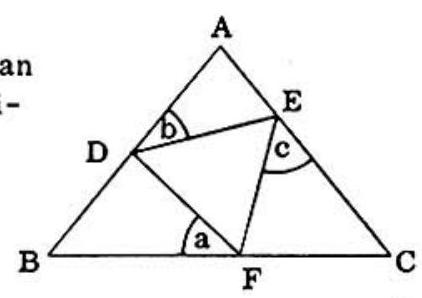
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 39: To satisfy the equation , and must be:
Answer Choices:
A. both rational
B. both real but not rational
C. both not real
D. one real, one not real
E. one real, one not real or both not real
Solution:
Problem 40: Given right triangle with legs 3 and 4. Find the length of the angle trisector to the hypotenuse nearer the shorter leg.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions