¶ 1970 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1970 AHSME problems, please refer below:
Problem 1: The fourth power of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A square and a circle have equal perimeters. The ratio of the area of the circle to the area of the square is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If and , then in terms of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let S be the set of all numbers which are the sum of the squares of three consecutive integers. Then we can say that
Answer Choices:
A. No member of S is divisible by 2
B. No member of S is divisible by 3 but some member is divisible by 11
C. No member of S is divisible by 3 or by 5
D. No member of S is divisible by 3 or by 7
E. None of these
Solution:
Problem 5: If , then , where , is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The smallest value of for real values of is
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 7: Inside square ABCD with side s, quarter-circle arcs with radii s and centers at A and B are drawn. These arcs intersect at a point X inside the square. How far is X from side CD?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: If and , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Points and are on line segment , and both points are on the same side of the midpoint of AB. Point P divides AB in the ratio and Q divides AB in the ratio . If , then the length of segment is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Let be an infinite repeating decimal with the digits 8 and 1 repeating. When F is written as a fraction in lowest terms, the denominator exceeds the numerator by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: If two factors of are and , the value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A circle with radius is tangent to sides , and of rectangle and passes through the midpoint of diagonal . The area of the rectangle, in terms of , is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Given the binary operation* defined by for all positive numbers and b. Then for all positive , we have
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 14: Consider where and are positive numbers. If the roots of this equation differ by 1, then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Lines in the -plane are drawn through the point and the trisection points of the line segment joining the points and . One of these lines has the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If is a function such that , and such that for , then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If , then for all and such that and , we have
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 18: is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The sum of an infinite geometric series with common ratio such that , is 15, and the sum of the squares of the terms of this series is 45. The first term of the series is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Lines and lie in a plane. is the midpoint of line segment , and BH and CK are perpendicular to HK. Then we
Answer Choices:
A. always have
B. always have
C. sometimes have but not always
D. always have
E. always have
Solution:
Problem 21: On an auto trip, the distance read from the instrument panel was 450 miles. With snow tires on for the return trip over the same route, the reading was 440 miles. Find, to the nearest hundredth of an inch, the increase in radius of the wheels if the original radius was 15 inches.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: If the sum of the first 3 n positive integers is 150 more than the sum of the first positive integers, then the sum of the first positive integers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The number ( 10 is written in base 10 ), when written in the base 12 system, ends with exactly zeros. The value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: An equilateral triangle and a regular hexagon have equal perimeters. If the area of the triangle is 2 , then the area of the hexagon is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: For every real number , let be the greatest integer which is less than or equal to . If the postal rate for first class mail is six cents for every ounce or portion thereof, then the cost in cents of first-class postage on a letter weighing ounces is always
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: The number of distinct points in the -plane common to the graphs of and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: In a triangle, the area is numerically equal to the perimeter. What is the radius of the inscribed circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: In triangle , the median from vertex is perpendicular to the median - from vertex . If the lengths of sides and are 6 and 7 respectively, then the length of side is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: It is now between 10:00 and 11:00 o'clock, and six minutes from now, the minute hand of a watch will be exactly opposite the place where the hour hand was three minutes ago. What is the exact time now?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: In the accompanying figure, segments AB and CD are parallel, the measure of angle is twice that of angle , and the measures of segments AD and CD are a and b respectively. Then the measure of is equal to
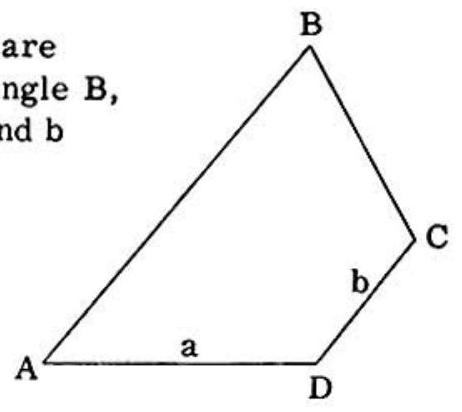
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: If a number is selected at random from the set of all five-digit numbers in which the sum of the digits is equal to 43 , what is the probability that this number will be divisible by 11 ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: A and B travel around a circular track at uniform speeds in opposite directions, starting from diametrically opposite points. If they start at the same time, meet first after B has travelled 100 yards, and meet a second time 60 yards before A completes one lap, then the circumference of the track in yards is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: Find the sum of the digits of all the numerals in the sequence .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: The greatest integer that will divide , and and leave the same remainder is
Answer Choices:
A.
B.
C.
D. an odd multiple of 7 greater than 49
E. an even multiple of 7 greater than 98
Solution:
Problem 35: A retiring employee receives an annual pension proportional to the square root of the number of years of his service. Had he served a years more, his pension would have been dollars greater, whereas, had he served b years more , his pension would have been dollars greater than the original annual pension. Find his annual pension in terms of , and .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions