¶ 1971 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1971 AHSME problems, please refer below:
Problem 1: The number of digits in the number is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If men take days to lay bricks, then the number of days it will take men working at the same rate to lay bricks, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If the point lies on the straight line joining the points and in the plane, then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: After simple interest for two months at per annum was credited, a Boy Scout Troop had a total of in the Council Treasury. The interest credited was a number of dollars plus the following number of cents
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Points , and lie on the circle shown and the measures of arcs and are and respectively. The sum of the measures of angles and is
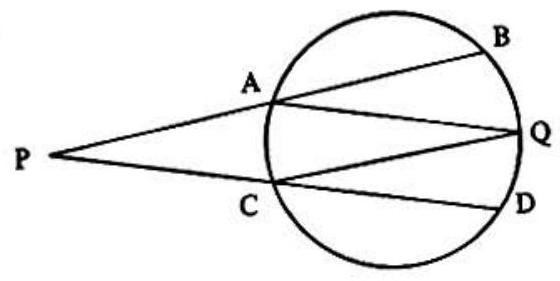
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 6: Let * be a symbol denoting the binary operation on the set of all non-zero real numbers as follows: For any two numbers and of . Then the one of the following statements which is not true, is
Answer Choices:
A. * is commutative over
B. is an identity element for in
C. is associative over
D. Every element of S has an inverse for *
E. is an inverse for of the element a of
Solution:
Problem 7: is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The solution set of is the set of all values of such that
Answer Choices:
A.
B.
C.
D. or
E. or
Solution:
Problem 9: An uncrossed belt is fitted without slack around two circular pulleys with radii of 14 inches and 4 inches. If the distance between the points of contact of the belt with the pulleys is 24 inches, then the distance between the centers of the pulleys in inches is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Each of a group of 50 girls is blonde or brunette and is blue or brown eyed. If 14 are blue-eyed blondes, 31 are brunettes, and 18 are brown-eyed, then the number of brown-eyed brunettes is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The numeral 47 in base a represents the same number as 74 in base b. Assuming that both bases are positive integers, the least possible value for written as a Roman numeral, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: For each integer , there is a mathematical system in which two or more integers are defined to be congruent if they leave the same non-negative remainder when divided by N . If 69,90 , and 125 are congruent in one such system, then in that same system, 81 is congruent to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If is evaluated correct to 5 decimal places, then the digit in the fifth decimal place is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The number is exactly divisible by two numbers between 60 and 70 . These numbers are
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: An aquarium on a level table has rectangular faces and is 10 inches wide and 8 inches high. When it was tilted, the water in it just covered an end but only three-fourths of the rectangular bottom. The depth of the water when the bottom was again made level was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: After finding the average of 35 scores, a student carelessly included the average with the 35 scores and found the average of these 36 numbers. The ratio of the second average to the true average was
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 17: A circular disk is divided by 2 n equally spaced radii and one secant line. The maximum number of non-overlapping areas into which the disk can be divided is
Answer Choices:
A.
B.
C.
D. 3 n
E.
Solution:
Problem 18: The current in a river is flowing steadily at 3 miles per hour. A motor boat which travels at a constant rate in still water goes downstream 4 miles and then returns to its starting point. The trip takes one hour, excluding the time spent in turning the boat around. The ratio of the downstream to the upstream rate is .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: If the line intersects the ellipse exactly once, then the value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The sum of the squares of the roots of the equation is 10 . The absolute value of is equal to
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 21: If , then the sum is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: If is one of the imaginary roots of the equation , then the product is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Teams and are playing a series of games. If the odds for either team to win any game are even and Team A must win two or Team B three games to win the series, then the odds favoring Team A to win the series are
Answer Choices:
A. 11 to 5
B. 5 to 2
C. 8 to 3
D. 3 to 2
E. 13 to 6
Solution:
Problem 24: Pascal's triangle is an array of positive integers (See figure), in which the first row is 1 , the second row is two l's, each row begins and ends with 1 , and the th number in any row when it is not 1 , is the sum of the th and th numbers in the immediately preceding row. The quotient of the number of numbers in the first rows which are not l's and the number of 1 's is
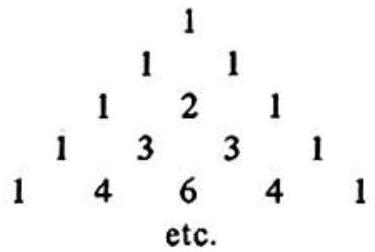
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 25: A teen age boy wrote his own age after his father's. From this new four place number he subtracted the absolute value of the difference of their ages to get 4,289 . The sum of their ages was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: In triangle , point divides side in the ratio . Let be the point of intersection of side and where is the midpoint of . Then point divides side in the ratio
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: A box contains chips, each of which is red, white, or blue. The number of blue chips is at least half the number of white chips, and at most one third the number of red chips. The number which are white or blue is at least 55 . The minimum number of red chips is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Nine lines parallel to the base of a triangle divide the other sides each into 10 equal segments and the area into 10 distinct parts. If the area of the largest of these parts is 38 , then the area of the original triangle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Given the progression . The least positive integer such that the product of the first n terms of the progression exceeds is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Given the linear fractional transformation of into . Define for . Assuming that , it follows that is equal to
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 31: Quadrilateral is inscribed in a circle with side , a diameter of length 4. If sides and each have length 1 , then side has length
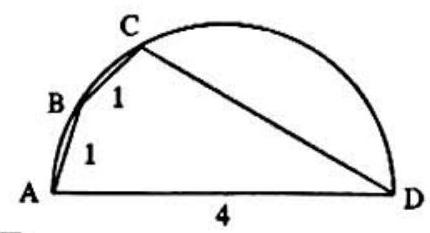
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: If , then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: If P is the product of quantities in Geometric Progression, S their sum, and the sum of their reciprocals, then in terms of , and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: An ordinary clock in a factory is running slow so that the minute hand passes the hour hand at the usual dial positions ( 12 o'clock, etc.) but only every 69 minutes. At time and onehalf for overtime, the extra pay to which a per hour worker should be entitled after working a normal 8 hour day by that slow running clock, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: Each circle in an infinite sequence with decreasing radii is tangent externally to the one following it and to both sides of a given right angle. The ratio of the area of the first circle to the sum of areas of all other circles in the sequence, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions