¶ 1997 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1997 AHSME problems, please refer below:
Problem 1: If and are digits for which
then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The adjacent sides of the decagon shown meet at right angles. What is its perimeter?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If , and are real numbers such that
then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: If is larger than , and is larger than , then is what percent larger than
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A rectangle with perimeter is divided into five congruent rectangles as shown in the diagram. What is the perimeter of one of the five congruent rectangles?
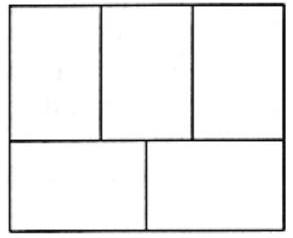
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Consider the sequence
whose term is . What is the average of the first terms of the sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The sum of seven integers is . What is the maximum number of the seven integers that can be larger than
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Mientka Publishing Company prices its best seller Where's Walter? as follows:
where is the number of books ordered, and is the cost in dollars of books. Notice that books cost less than books. For how many values of is it cheaper to buy more than books than to buy exactly books?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In the figure, is a square, is the midpoint of , and is on . If is perpendicular to , then the area of quadrilateral is
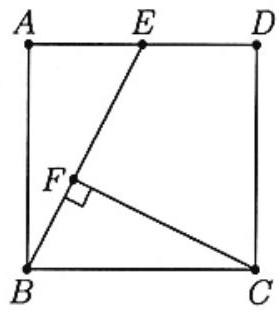
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Two six-sided dice are fair in the sense that each face is equally likely to turn up. However, one of the dice has the replaced by and the other die has the replaced by . When these dice are rolled, what is the probability that the sum is an odd number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: In the sixth, seventh, eighth, and ninth basketball games of the season, a player scored , and points, respectively. Her points-per-game average was higher after nine games than it was after the first five games. If her average after ten games was greater than , what is the least number of points she could have scored in the tenth game?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If and are real numbers and , then the line whose equation is contain the point
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many two-digit positive integers have the property that the sum of and the number obtained by reversing the order of the digits of is a perfect square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The number of geese in a flock increases so that the difference between the populations in year and year is directly proportional to the population in year . If the populations in the years and were and respectively, then the population in was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Medians and of triangle are perpendicular, , and . The area of triangle is
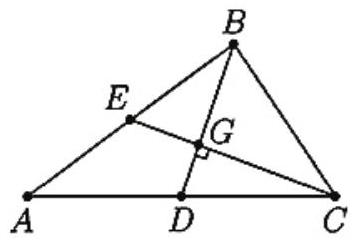
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The three row sums and the three column sums of the array
are the same. What is the least number of entries that must be altered to make all six sums different from one another?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A line intersects the graph of and the graph of . The distance between the points of intersection is . Given that , where and are integers, what is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A list of integers has mode and mean . The smallest number in the list is . The median of the list is a member of the list. If the list member were replaced by , the mean and median of the new list would be and , respectively. If were instead replaced by , the median of the new list would be . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A circle with center is tangent to the coordinate axes and to the hypotenuse of the triangle as shown, where . To the nearest hundredth, what is the radius of the circle?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Which one of the following integers can be expressed as the sum of consecutive positive integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: For any positive integer , let
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Ashley, Betty, Carlos, Dick, and Elgin went shopping. Each had a whole number of dollars to spend, and together they had . The absolute difference between the amounts Ashley and Betty had to spend was . The absolute difference between the amounts Betty and Carlos had was , between Carlos and Dick was , between Dick and Elgin was , and between Elgin and Ashley was . How much did Elgin have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: In the figure, polygons , and are isosceles right triangles; , and are squares with sides of length ; and is an equilateral triangle. The figure can be folded along its edges to form a polyhedron having the polygons as faces. The volume of this polyhedron is
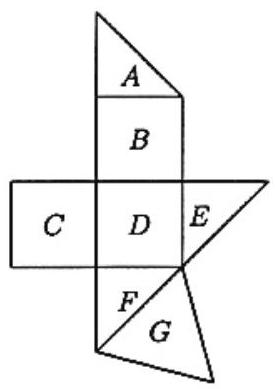
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A rising number, such as , is a positive integer each digit of which is larger than each of the digits to its left. There are five-digit rising numbers. When these numbers are arranged from smallest to largest, the number in the list does not contain the digit
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a parallelogram and let , and be parallel rays in space on the same side of the plane determined by . If , , and and are the midpoints of and , respectively, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Triangle and point in the same plane are given. Point is equidistant from and , angle is twice angle , and intersects at point . If and , then
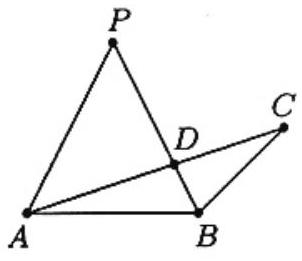
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Consider those functions that satisfy for all real . Any such function is periodic, and there is a least common positive period for all of them. Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: How many ordered triples of integers satisfy
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Call a positive real number special if it has a decimal representation that consists entirely of digits and . For example, and are special numbers. What is the smallest such that can be written as a sum of special numbers?
Answer Choices:
A.
B.
C.
D.
E. cannot be represented as a sum of finitely many special numbers
Solution:
Problem 30: For positive integers , denote by the number of pairs of different adjacent digits in the binary (base two) representation of . For example, , and . For how many positive integers less than or equal to does
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions