¶ 2021 AMC 10A_Spring Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2021 AMC 10A_Spring problems here.
Discussion Forum
Engage in discussion about the 2021 AMC 10A_Spring math contest by visiting Random Math AMC 10A_Spring 2021 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2021 AMC 10A_Spring problems, please refer below:
Problem 1: What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Portia's high school has times as many students as Lara's high school. The two high schools have a total of students. How many students does Portia's high school have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The sum of two natural numbers is . One of the two numbers is divisible by . If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A cart rolls down a hill, traveling inches the first second and accelerating so that during each successive -second time interval, it travels inches more than during the previous -second interval. The cart takes seconds to reach the bottom of the hill. How far, in inches, does it travel?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The quiz scores of a class with students have a mean of . The mean of a collection of of these quiz scores is . What is the mean of the remaining quiz scores in terms of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Chantal and Jean start hiking from a trailhead toward a fire tower. Jean is wearing a heavy backpack and walks slower. Chantal starts walking at miles per hour. Halfway to the tower, the trail becomes really steep, and Chantal slows down to miles per hour. After reaching the tower, she immediately turns around and descends the steep part of the trail at miles per hour. She meets Jean at the halfway point. What was Jean's average speed, in miles per hour, until they meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Tom has a collection of snakes, of which are purple and of which are happy. He observes that:
-
all of his happy snakes can add,
-
none of his purple snakes can subtract, and
-
all of his snakes that can't subtract also can't add.
Which of these conclusions can be drawn about Tom's snakes?
Answer Choices:
A. Purple snakes can add
B. Purple snakes are happy
C. Snakes that can add are purple
D. Happy snakes are not purple
E. Happy snakes can't subtract
Solution:
Problem 8: When a student multiplied the number by the repeating decimal,
where and are digits, he did not notice the notation and just multiplied times Later he found that his answer is less than the correct answer. What is the -digit number
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: What is the least possible value of for real numbers and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Which of the following is equivalent to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: For which of the following integers is the base- number not divisible by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the tops of the liquid surfaces are and . Into each cone is dropped a spherical marble of radius , which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level in the narrow cone to the rise of the liquid level in the wide cone?
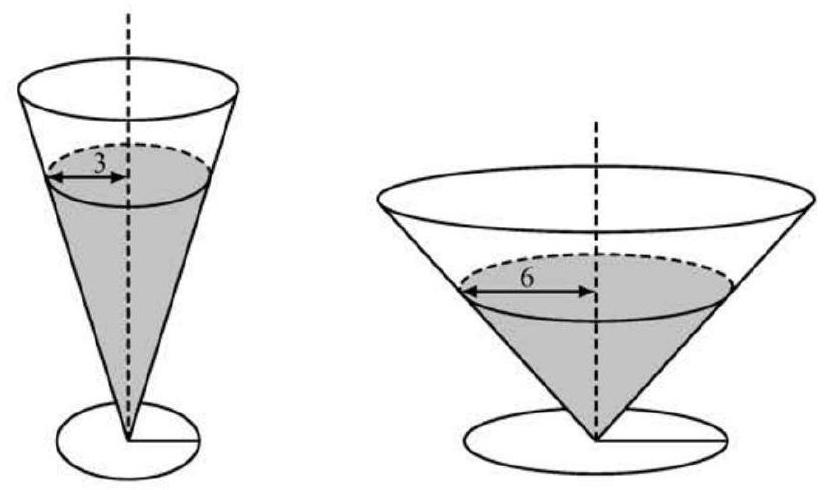
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: What is the volume of tetrahedron with edge lengths , , and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: All the roots of polynomial are positive integers, possibly repeated. What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Values for , and are to be selected from without replacement (i.e., no two letters have the same value). How many ways are there to make such choices so that the two curves and intersect? (The order in which the curves are listed does not matter; for example, the choices is considered the same as the choices .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In the following list of numbers, the integer appears times in the list for .
What is the median of the numbers in this list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Trapezoid has , and . Let be the intersection of the diagonals and , and let be the midpoint of . Given that , the length can be written in the form , where and are positive integers and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be a function defined on the set of positive rational numbers with the property that for all positive rational numbers and . Furthermore, suppose that also has the property that for every prime number . For which of the following numbers is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The area of the region bounded by the graph of
is , where and are integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In how many ways can the sequence be rearranged so that no three consecutive terms are increasing and no three consecutive terms are decreasing?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let be an equiangular hexagon. The lines , and determine a triangle with area , and the lines , and determine a triangle with area . The perimeter of hexagon can be expressed as , where , and are positive integers and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Hiram's algebra notes are pages long and are printed on sheets of paper; the first sheet contains pages and , the second sheet contains pages and , and so on. One day he leaves his notes on the table before leaving for lunch, and his roommate decides to borrow some pages from the middle of the notes. When Hiram comes back, he discovers that his roommate has taken a consecutive set of sheets from the notes and that the average (mean) of the page numbers on all remaining sheets is exactly . How many sheets were borrowed?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Frieda the frog begins a sequence of hops on a grid of squares, moving one square on each hop and choosing at random the direction of each hop-up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she wraps around and jumps to the opposite edge. For example if Frieda begins in the center square and makes two hops up, the first hop would place her in the top row middle square, and the second hop would cause Frieda to jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping if she lands on a corner square. What is the probability that she reaches a corner square on one of the four hops?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The interior of a quadrilateral is bounded by the graphs of and , where is a positive real number. What is the area of this region in terms of , valid for all ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: How many ways are there to place indistinguishable red chips, indistinguishable blue chips, and indistinguishable green chips in the squares of a grid so that no two chips of the same color are directly adjacent to each other, either vertically or horizontally?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions