¶ 2024 AMC10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2024 AMC10B problems here.
Discussion Forum
Engage in discussion about the 2024 AMC10B math contest by visiting Random Math AMC10B 2024 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2024 AMC10B problems, please refer below:
Problem 1: In a long line of people arranged left to right, the 1013 th person from the left is also the 1010th person from the right. How many people are in the line?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: For how many integer values of is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Balls numbered are deposited in 5 bins, labeled , and E , using the following procedure. Ball 1 is deposited in bin A, and balls 2 and 3 are deposited in bin B . The next 3 balls are deposited in bin C , the next 4 in bin D , and so on, cycling back to bin A after balls are deposited in bin E. (For example, balls numbered 22, 23, ... 28 are deposited in bin B at step 7 of this process.) In which bin is ball 2024 deposited?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In the following expression, Melanie changed some of the plus signs to minus signs:
When the new expression was evaluated, it was negative. What is the least number of plus signs that Melanie could have changed to minus signs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A rectangle has integer length sides and an area of 2024 . What is the least possible perimeter of the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: What is the remainder when is divided by 19 ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let be the product of all the positive integer divisors of 42 . What is the units digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Real numbers , and have arithmetic mean 0 . The arithmetic mean of , and is 10 . What is the arithmetic mean of , and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Quadrilateral is a parallelogram, and is the midpoint of the side . Let be the intersection of lines and . What is the ratio of the area of quadrilateral to the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: In the figure below is a rectangle with and . Point lies on , point lies on , and is a right angle. The areas of triangles and are equal. What is the area of ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A group of 100 students from different countries meet at a mathematics competition. Each student speaks the same number of languages, and, for every pair of students A and B, student A speaks some language that student B does not speak, and student B speaks some language that student A does not speak. What is the least possible total number of languages spoken by all the students?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Positive integers and satisfy the equation . What is the minimum possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A dartboard is the region in the coordinate plane consisting of points such that . A target is the region where . A dart is thrown and lands at a random point in . The probability that the dart lands in can be expressed as , where and are relatively prime positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A list of 9 real numbers consists of , and 7 , as well as , and with . The range of the list is 7 , and the mean and the median are both positive integers. How many ordered triples are possible?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 16: Jerry likes to play with numbers. One day, he wrote all the integers from 1 to 2024 on the whiteboard. Then he repeatedly chose four numbers on the whiteboard, erased them, and replaced them by either their sum or their product. (For example, Jerry's first step might have been to erase 1, 2, 3, and 5, and then write either 11 , their sum, or 30 , their product, on the whiteboard.) After repeatedly performing this operation, Jerry noticed that all the remaining numbers on the whiteboard were odd. What is the maximum possible number of integers on the whiteboard at that time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In a race among 5 snails, there is at most one tie, but that tie can involve any number of snails. For example, the result of the race might be that Dazzler is first; Abby, Cyrus, and Elroy are tied for second; and Bruna is fifth. How many different results of the race are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: How many different remainders can result when the 100th power of an integer is divided by 125 ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In the following table, each question mark is to be replaced by "Possible" or "Not Possible" to indicate whether a nonvertical line with the given slope can contain the given number of lattice points (points both of whose coordinates are integers). How many of the 12 entries will be "Possible"?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Three different pairs of shoes are placed in a row so that no left shoe is next to a right shoe from a different pair. In how many ways can these six shoes be lined up?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two straight pipes (circular cylinders), with radii 1 and , lie parallel and in contact on a flat floor. The figure below shows a head-on view. What is the sum of the possible radii of a third parallel pipe lying on the same floor and in contact with both?
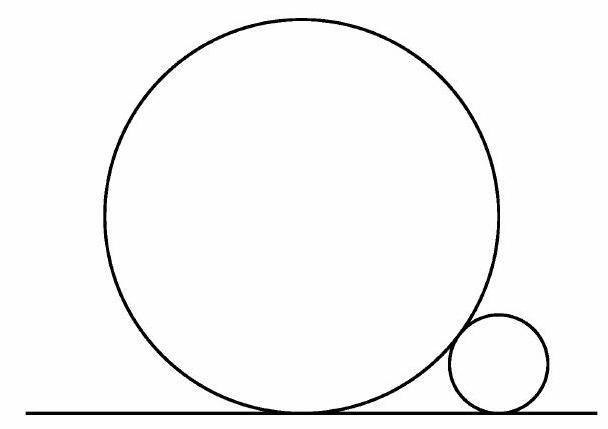
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A group of 16 people will be partitioned into 4 indistinguishable 4-person committees. Each committee will have one chairperson and one secretary. The number of different ways to make these assignments can be written as , where and are positive integers and is not divisible by 3 . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The Fibonacci numbers are defined by , and for . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let
How many of the values , and are integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Each of 27 bricks (right rectangular prisms) has dimensions , where , and are pairwise relatively prime positive integers. These bricks are arranged to form a block, as shown on the left below. A 28th brick with the same dimensions is introduced, and these bricks are reconfigured into a block, shown on the right. The new block is 1 unit taller, 1 unit wider, and 1 unit deeper than the old one. What is ?
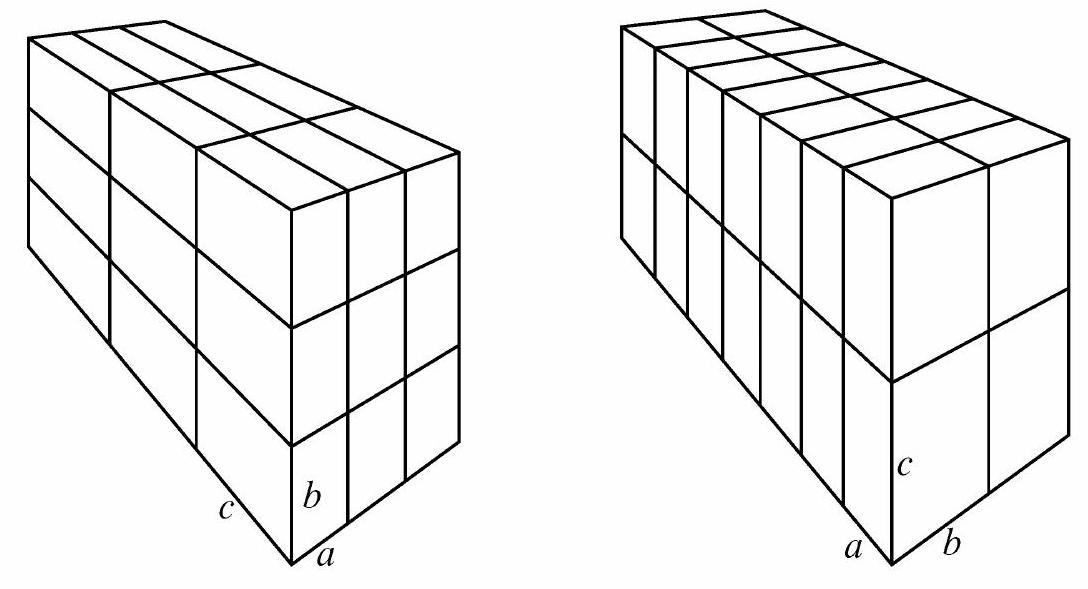
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions