¶ 2001 AMC 12 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2001 AMC 12 problems here.
Discussion Forum
Engage in discussion about the 2001 AMC 12 math contest by visiting Random Math AMC 12 2001 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2001 AMC 12 problems, please refer below:
Problem 1: The sum of two numbers is . Suppose is added to each number and then each of the resulting numbers is doubled. What is the sum of the final two numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Let and denote the product and the sum, respectively, of the digits of the integer . For example, and . Suppose is a two-digit number such that . What is the units digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The state income tax where Kristin lives is levied at the rate of of the first of annual income plus of any amount above . Kristin noticed that the state income tax she paid amounted to of her annual income. What was her annual income?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The mean of three numbers is more than the least of the numbers and less than the greatest. The median of the three numbers is . What is their sum?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: What is the product of all positive odd integers less than ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A telephone number has the form , where each letter represents a different digit. The digits in each part of the number are in decreasing order; that is, , and . Furthermore, , and are consecutive even digits; , and are consecutive odd digits; and . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: A charity sells benefit tickets for a total of . Some tickets sell for full price (a whole dollar amount), and the rest sell for half price. How much money is raised by the full-price tickets?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Which of the cones below can be formed from a sector of a circle of radius by aligning the two straight sides?
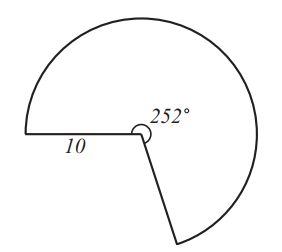
Answer Choices:
A. .jpg)
B. 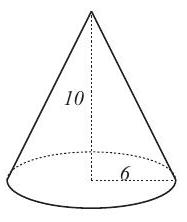
C. 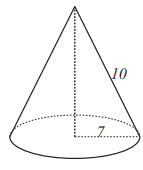
D. .jpg)
E. 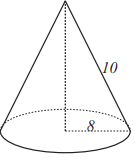
Solution:
Problem 9: Let be a function satisfying for all positive real numbers and . If , what is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The plane is tiled by congruent squares and congruent pentagons as indicated. The percent of the plane that is enclosed by the pentagons is closest to
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A box contains exactly five chips, three red and two white. Chips are randomly removed one at a time without replacement until all the red chips are drawn or all the white chips are drawn. What is the probability that the last chip drawn is white?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: How many positive integers not exceeding are multiples of or but not ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The parabola with equation and vertex is reflected about the line . This results in the parabola with equation . Which of the following equals ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Given the nine-sided regular polygon , how many distinct equilateral triangles in the plane of the polygon have at least two vertices in the set ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: An insect lives on the surface of a regular tetrahedron with edges of length . It wishes to travel on the surface of the tetrahedron from the midpoint of one edge to the midpoint of the opposite edge. What is the length of the shortest such trip? (Note: Two edges of a tetrahedron are opposite if they have no common endpoint.)
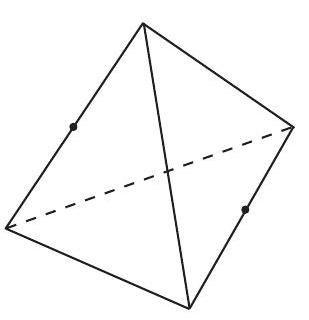
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A spider has one sock and one shoe for each of its eight legs. In how many different orders can the spider put on its socks and shoes, assuming that, on each leg, the sock must be put on before the shoe?
Answer Choices:
A.
B. !$
C.
D.
E.
Solution:
Problem 17: A point is selected at random from the interior of the pentagon with vertices , and . What is the probability that is obtuse?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A circle centered at with a radius of and a circle centered at with a radius of are externally tangent. A third circle is tangent to the first two and to one of their common external tangents as shown. The radius of the third circle is
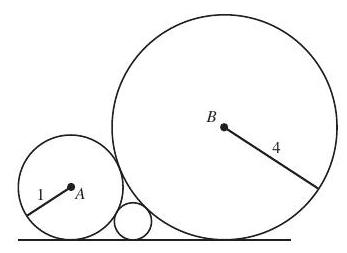
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The polynomial has the property that the mean of its zeros, the product of its zeros, and the sum of its coefficients are all equal. If the -intercept of the graph of is 2 , what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Points , and lie in the first quadrant and are the vertices of quadrilateral . The quadrilateral formed by joining the midpoints of , and is a square. What is the sum of the coordinates of point ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Four positive integers , and have a product of ! and satisfy
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: In rectangle , points and lie on so that and is the midpoint of . Also, intersects at and at . The area of rectangle is . Find the area of triangle .
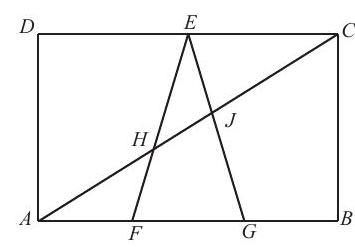
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A polynomial of degree four with leading coefficient and integer coefficients has two real zeros, both of which are integers. Which of the following can also be a zero of the polynomial?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: In triangle . Point is on so that and . Find .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Consider sequences of positive real numbers of the form , in which every term after the first is less than the product of its two immediate neighbors. For how many different values of does the term appear somewhere in the sequence?
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions