¶ 2000 AMC 12 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2000 AMC 12 problems here.
Discussion Forum
Engage in discussion about the 2000 AMC 12 math contest by visiting Random Math AMC 12 2000 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2000 AMC 12 problems, please refer below:
Problem 1: In the year , the United States will host the International Mathematical Olympiad. Let , and be distinct positive integers such that the product . What is the largest possible value of the sum ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Each day, Jenny ate of the jellybeans that were in her jar at the beginning of that day. At the end of second day, remained. How many jellybeans were in the jar originally?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The Fibonacci sequence starts with two s, and each term afterwards is the sum of its two predecessors. Which one of the ten digits is the last to appear in the units position of a number in the Fibonacci sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If , where , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Two different prime numbers between and are chosen. When their sum is subtracted from their product, which of the following number could be obtained?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: How many positive integers have the property that is a positive integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Figure , and consist of , and nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure ?
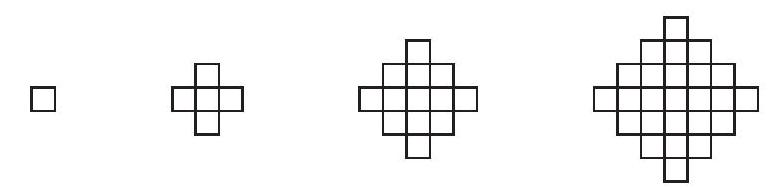
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Mrs.Walter gave an exam in a mathematics class of five students. She entered the scores in random order into a spreadsheet, which recalculated the class average after each score was entered. Mrs. Walter noticed that after each score was entered, the average was always an integer. The scores (listed in ascending order) were , and . What was the last scores Mrs.Walter entered?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The point is reflected in the -plane, then its image is rotated by about the -axis to produce , and finally, is translated by 5 units in the positive- direction to produce . What are the coordinates of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Two non-zero real numbers, and , satisfy . Find a possible value of .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let , and be nonnegative integers such that . What is the maximum value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: One morning each member of Angela's family drank an -ounce mixture of coffee with milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. How many people are in the family?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: When the mean, median, and mode of the list
are arranged in increasing order, they form a non-constant arithmetic progression. What is the sum of all possible real value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let be a function for which . Find the sum of all values of for which .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A checkerboard of rows and columns has a number written in each square, beginning in the upper left corner, so that the first row is numbered , the second row , and so on down the board. If the board is renumbered so that the left column, top to bottom, is , the second column and so on across the board, some square have the same numbers in both numbering systems. Find the sum of the numbers in these squares (under either system).
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A circle centered at has radius and contains the point . Segment is tangent to the circle at and . If point lies on and bisects , then
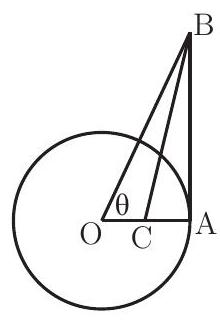
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: In year , the day of the year is a Tuesday. In year , the day is also a Tuesday. On what day of the week did the day of year occur?
Answer Choices:
A. Thursday
B. Friday
C. Saturday
D. Sunday
E. Monday
Solution:
Problem 19: In triangle , and . Let denote the midpoint of and let denote the intersection of with the bisector of angle . Which of the following is closest to the area of the triangle ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If , and are positive numbers satisfying
then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Through a point on the hypotenuse of a right triangle, lines are drawn parallel to the legs of the triangle so that the triangle is divided into a square and two smaller right triangles. The area of one of the two small right triangle is times the area of the square. The ratio of the area of the other small right triangle to the area of the square is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The graph below shows a portion of the curve defined by the quartic polynomial . Which of the following is the smallest?
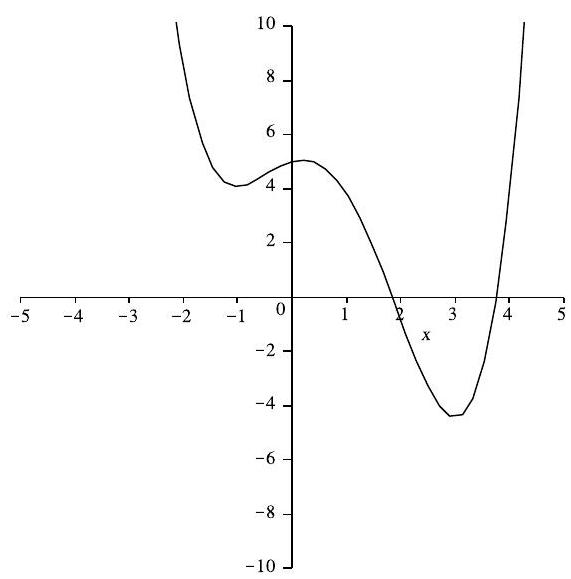
Answer Choices:
A.
B. The product of the zeros of
C. The product of the non-real zeros of
D. The sum of the coefficients of
E. The sum of the real zeros of
Solution:
Problem 23: Professor Gamble buys a lottery ticket, which requires that he pick six different integers from through , inclusive. He chooses his numbers so that the sum of the base-ten logarithms of his six numbers is an integer. It so happens that the integers on the winning ticket have the same property- the sum of the base-ten logarithms is an integer. What is the probability that Professor Gamble holds the winner ticket?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: If circular arcs and have centers at and , respectively, then there exists a circle tangent to both and , and to . If the length of is , then the circumference of the circle is
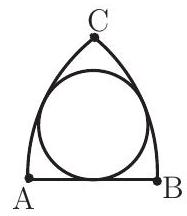
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Eight congruent equilateral triangles, each of a different color, are used to construct a regular octahedron. How many distinguishable ways are there to construct the octahedron? (Two colored octahedrons are distinguishable if neither can be rotated to look just like the other.)
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions