¶ 2007 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2007 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2007 AMC8 math contest by visiting Random Math 2007 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2007 AMC8 problems, please refer below:
Problem 1: Theresa's parents have agreed to buy her tickets to see her favorite band if she spends an average of hours per week helping around the house for weeks. For the first weeks she helps around the house for and hours. How many hours must she work during the final week to earn the tickets?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Six-hundred fifty students were surveyed about their pasta preferences. The choices were lasagna, manicotti, ravioli and spaghetti. The results of the survey are displayed in the bar graph. What is the ratio of the number of students who preferred spaghetti to the number of students who preferred manicotti?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: What is the sum of the two smallest prime factors of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A haunted house has six windows. In how many ways can Georgie the Ghost enter the house by one window and leave by a different window?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Chandler wants to buy a mountain bike. For his birthday, his grandparents send him , his aunt sends him and his cousin gives him . He earns per week for his paper route. He will use all of his birthday money and all of the money he earns from his paper route. In how many weeks will he be able to buy the mountain bike?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The average cost of a long-distance call in the USA in was cents per minute, and the average cost of a long-distance call in the USA in was cents per minute. Find the approximate percent decrease in the cost per minute of a longdistance call.

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The average age of people in a room is years. An -year-old person leaves the room. What is the average age of the four remaining people?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: In trapezoid is perpendicular to , , and . In addition, is on , and is parallel to . Find the area of .
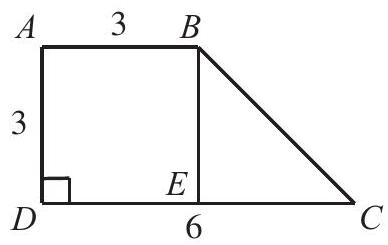
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: To complete the grid below, each of the digits through must occur once in each row and once in each column. What number will occupy the lower right-hand square?
.jpg)
Answer Choices:
A.
B.
C.
D.
E. cannot be determined
Solution:
Problem 10: For any positive integer , define to be the sum of the positive factors of . For example, . Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Tiles and are translated so one tile coincides with each of the rectangles and . In the final arrangement, the two numbers on any side common to two adjacent tiles must be the same. Which of the tiles is translated to Rectangle
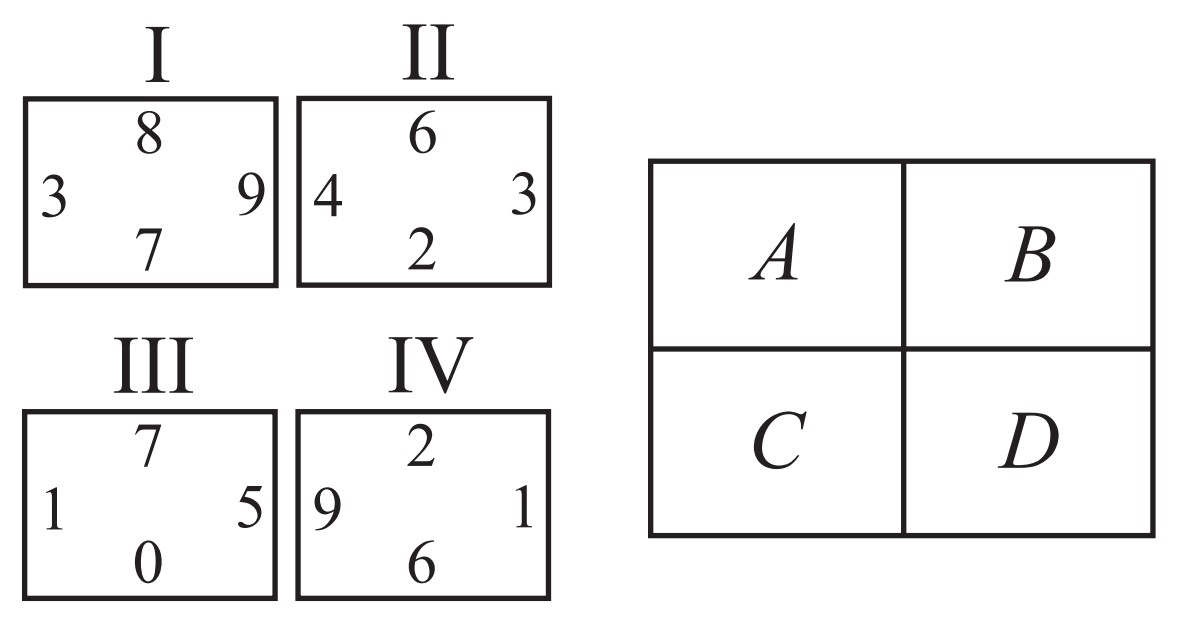
Answer Choices:
A.
B.
C.
D.
E. cannot be determined
Solution:
Problem 12: A unit hexagram is composed of a regular hexagon of side length and its equilateral triangular extensions, as shown in the diagram. What is the ratio of the area of the extensions to the area of the original hexagon?
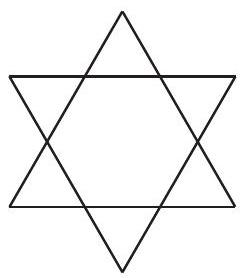
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Sets and , shown in the Venn diagram, have the same number of elements. Their union has elements and their intersection has elements. Find the number of elements in .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The base of isosceles is and its area is . What is the length of one of the congruent sides?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let and be numbers with . Which of the following is impossible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Amanda Reckonwith draws five circles with radii and . Then for each circle she plots the point , where is its circumference and is its area. Which of the following could be her graph?
Answer Choices:
A.
.jpg)
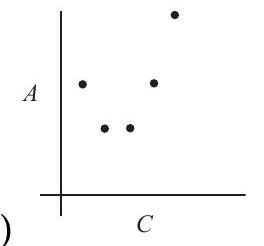
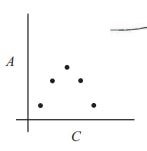
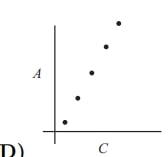
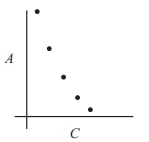
Solution:
Problem 17: A mixture of liters of paint is red tint, yellow tint and water. Five liters of yellow tint are added to the original mixture. What is the percent of yellow tint in the new mixture?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The product of the two -digit numbers
has thousands digit and units digit . What is the sum of and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Pick two consecutive positive integers whose sum is less than . Square both of those integers and then find the difference of the squares. Which of the following could be the difference?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Before district play, the Unicorns had won of their basketball games. During district play, they won six more games and lost two, to finish the season having won half their games. How many games did the Unicorns play in all?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two cards are dealt from a deck of four red cards labeled and four green cards labeled . A winning pair is two of the same color or two of the same letter. What is the probability of drawing a winning pair?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A lemming sits at a corner of a square with side length meters. The lemming runs meters along a diagonal toward the opposite corner. It stops, makes a right turn and runs more meters. A scientist measures the shortest distance between the lemming and each side of the square. What is the average of these four distances in meters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: What is the area of the shaded pinwheel shown in the grid?
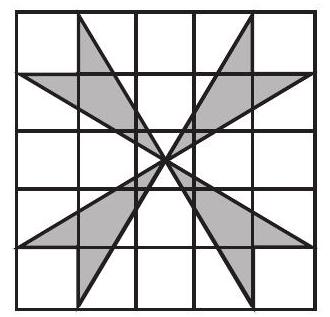
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A bag contains four pieces of paper, each labeled with one of the digits or , with no repeats. Three of these pieces are drawn, one at a time without replacement, to construct a three-digit number. What is the probability that the three-digit number is a multiple of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: On the dart board shown in the figure, the outer circle has radius and the inner circle has radius . Three radii divide each circle into three congruent regions, with point values shown. The probability that a dart will hit a given region is proportional to the area of the region. When two darts hit this board, the score is the sum of the point values in the regions. What is the probability that the score is odd?
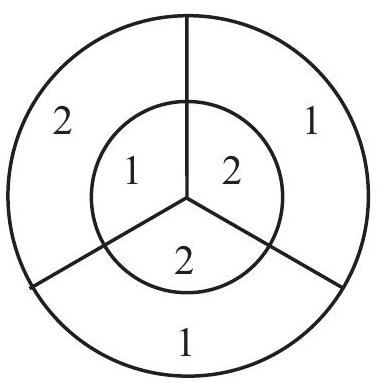
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions