¶ 2022 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2022 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2022 AMC8 math contest by visiting Random Math 2022 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2022 AMC8 problems, please refer below:
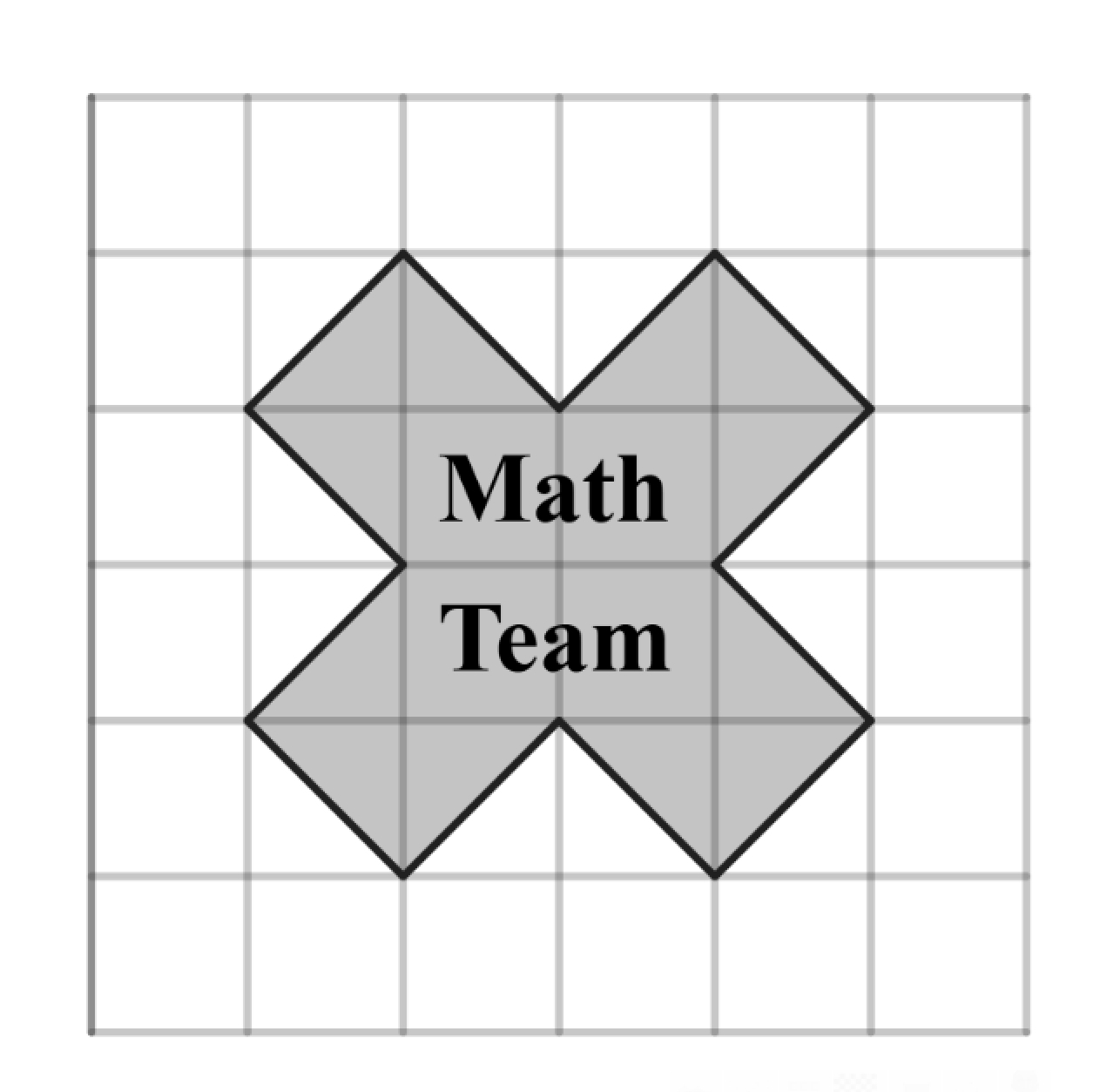
Problem 1: The Math Team designed a logo shaped like a multiplication symbol, shown below on a grid of -inch squares. What is the area of the logo in square inches?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Consider these two operations:
Compute the value:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: When three positive integers and are multiplied together, their product is . Suppose . In how many ways can the numbers be chosen?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
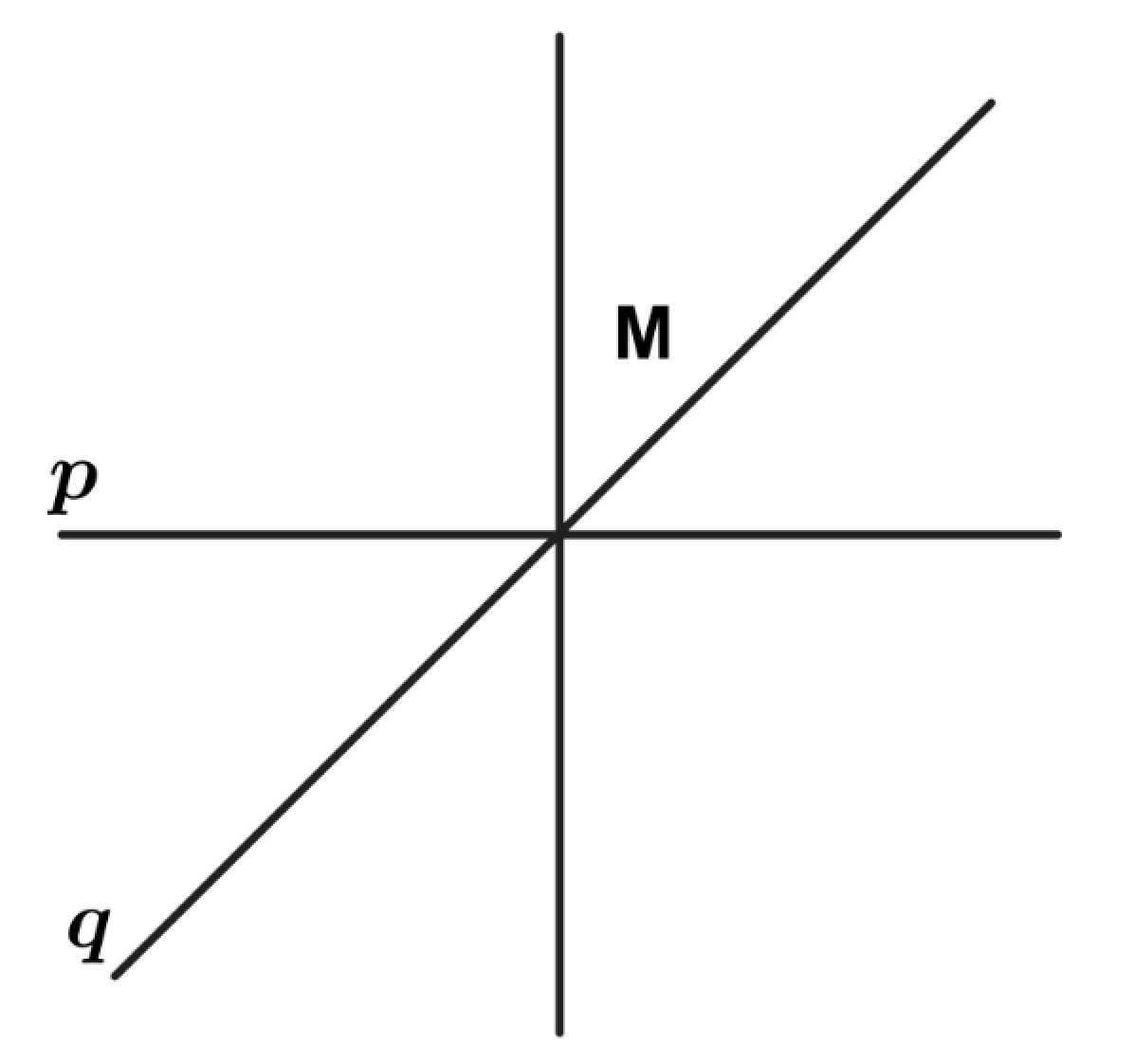
Problem 4: The letter in the figure below is first reflected over the line and then reflected over the line . What is the resulting image?
Answer Choices:
A. 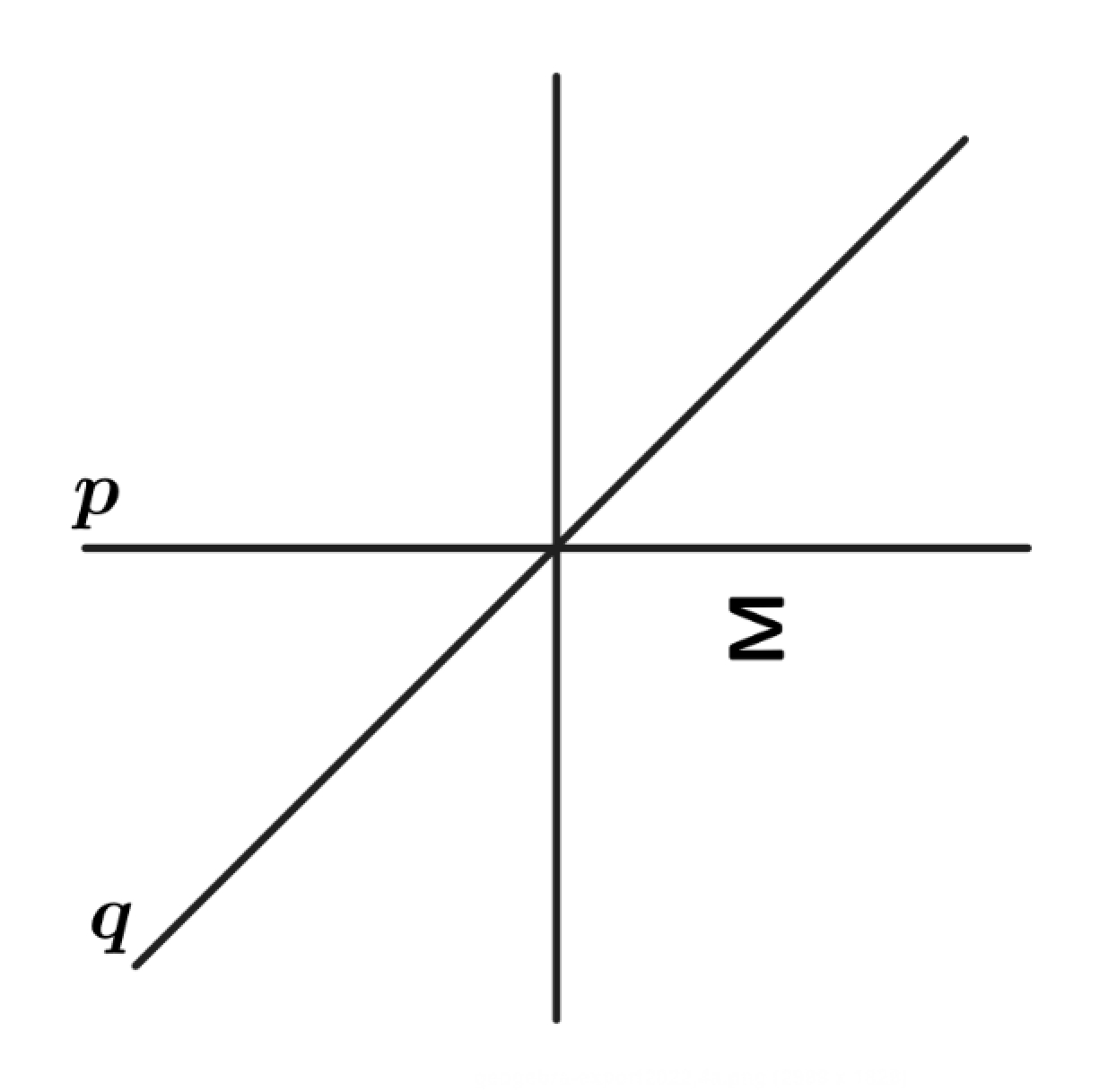
B. 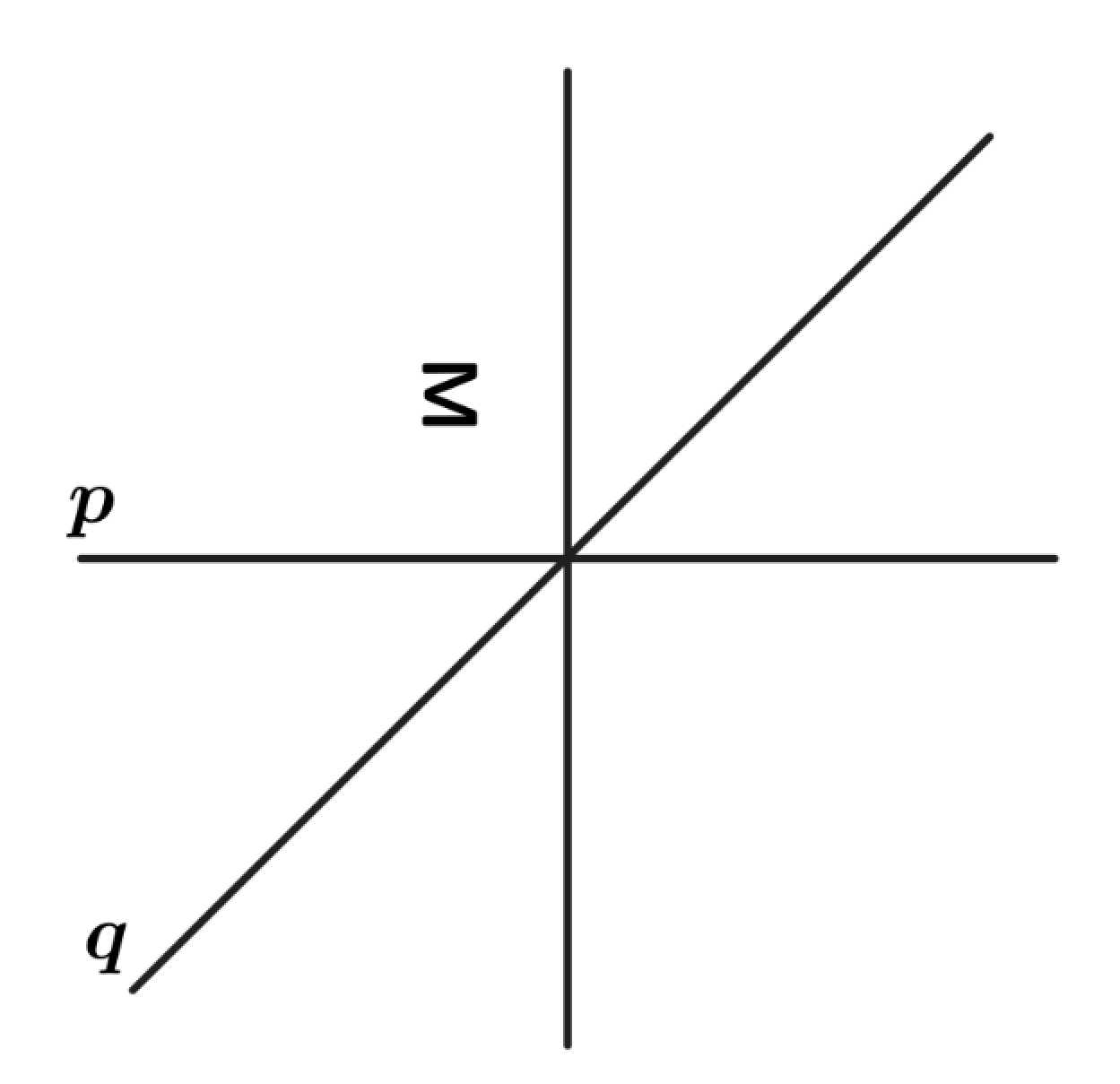
C. 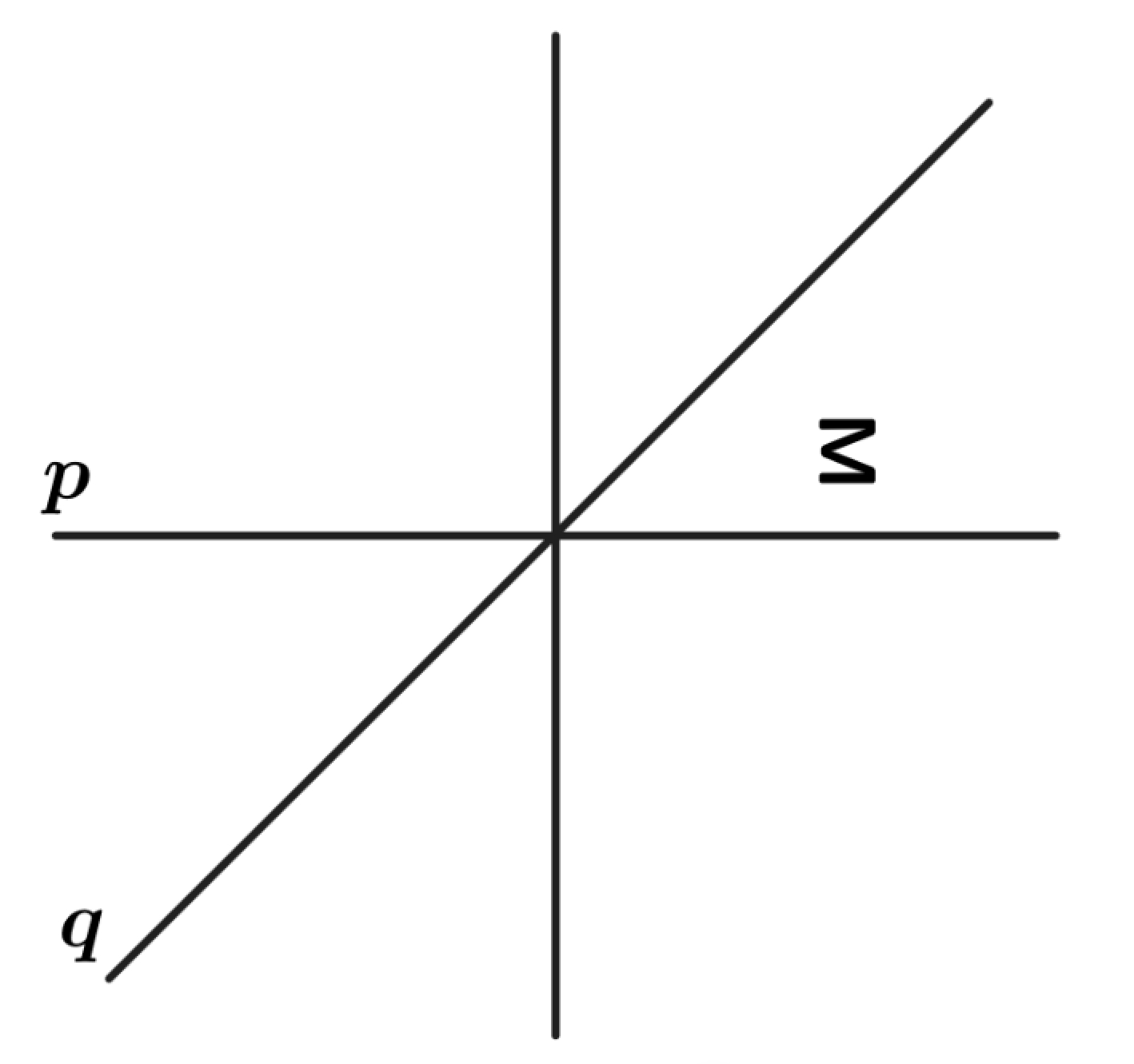
D. 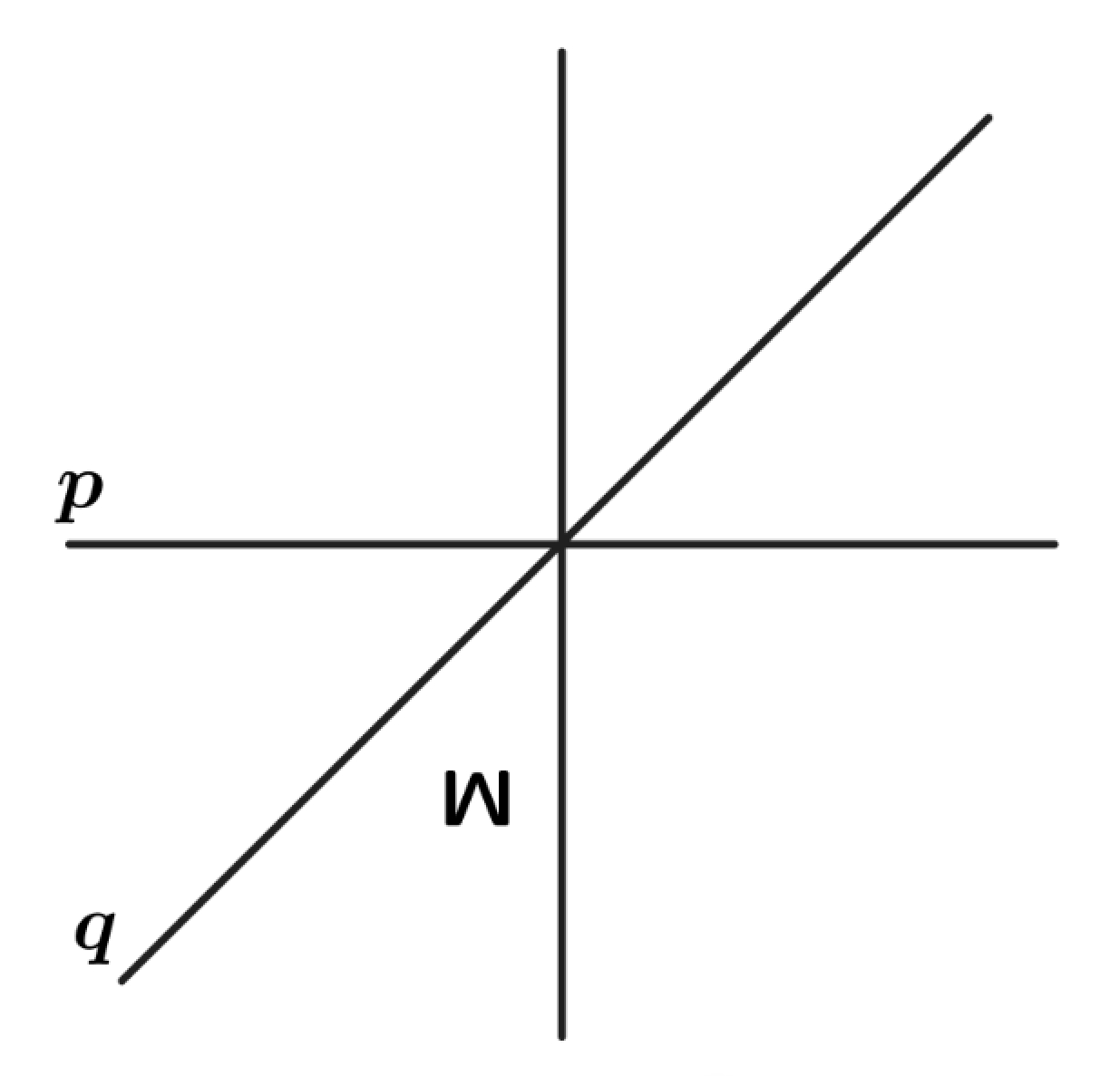
E. 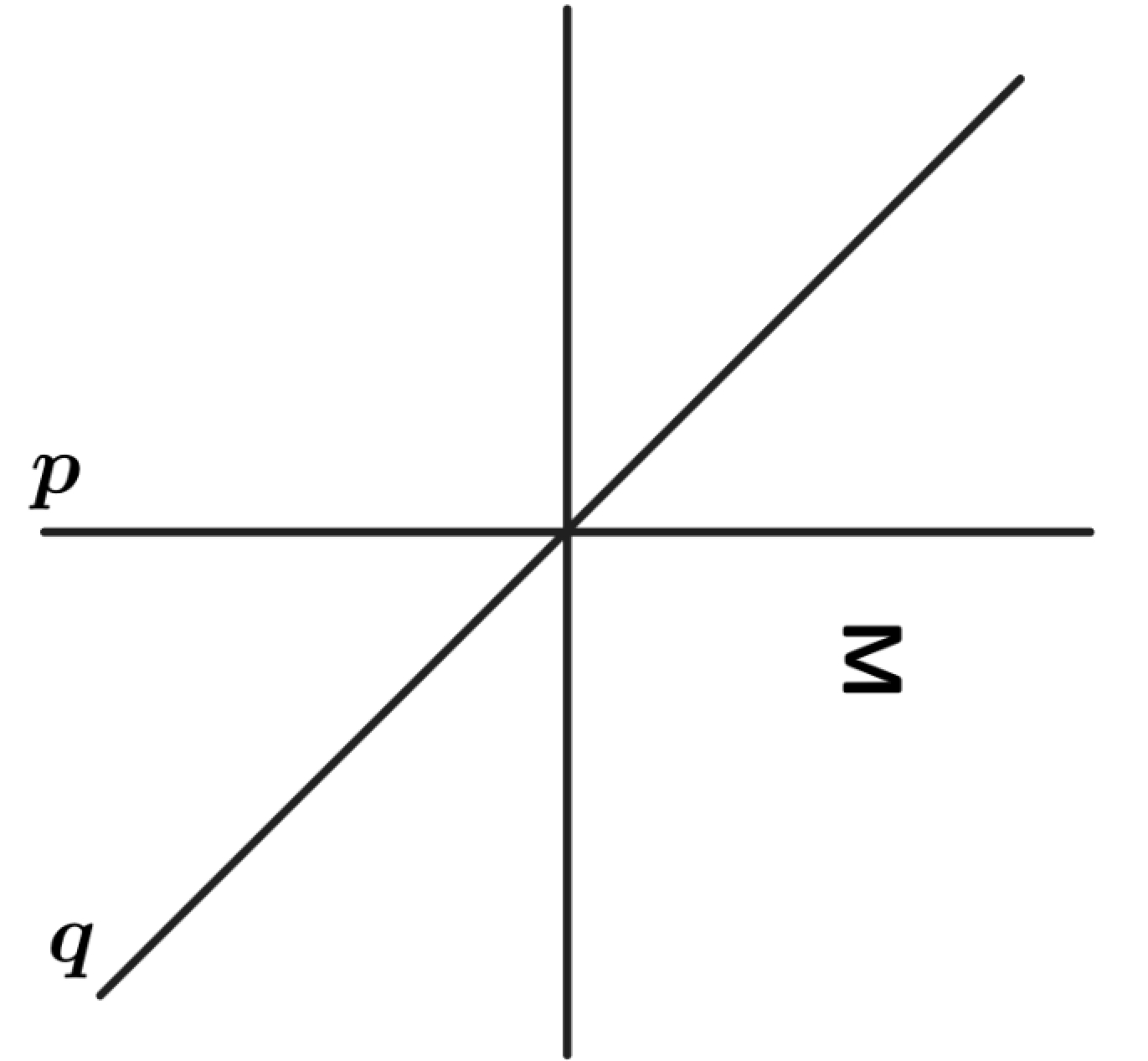
Solution:
Problem 5: Anna and Bella are celebrating their birthdays together. Five years ago, when Bella turned years old, she received a newborn kitten as a birthday present. Today the sum of the ages of the two children and the kitten is years. How many years older than Bella is Anna?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Three positive integers are equally spaced on a number line. The middle number is and the largest number is times the smallest number. What is the smallest of these three numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: When the World Wide Web first became popular in the , download speeds reached a maximum of about kilobits per second. Approximately how many minutes would the download of a megabyte song have taken at that speed? (Note that there are kilobits in a megabyte.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: What is the value of:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A cup of boiling water () is placed to cool in a room whose temperature remains constant at . Suppose the difference between the water temperature and the room temperature is halved every minutes.What is the water temperature, in degrees Fahrenheit, after minutes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: One sunny day, Ling decided to take a hike in the mountains. She left her house at a.m., drove at a constant speed of miles per hour, and arrived at the hiking trail at a.m. After hiking for hours, Ling drove home at a constant speed of miles per hour. Which of the following graphs best illustrates the distance between Ling’s car and her house over the course of her trip?
Answer Choices:
A. 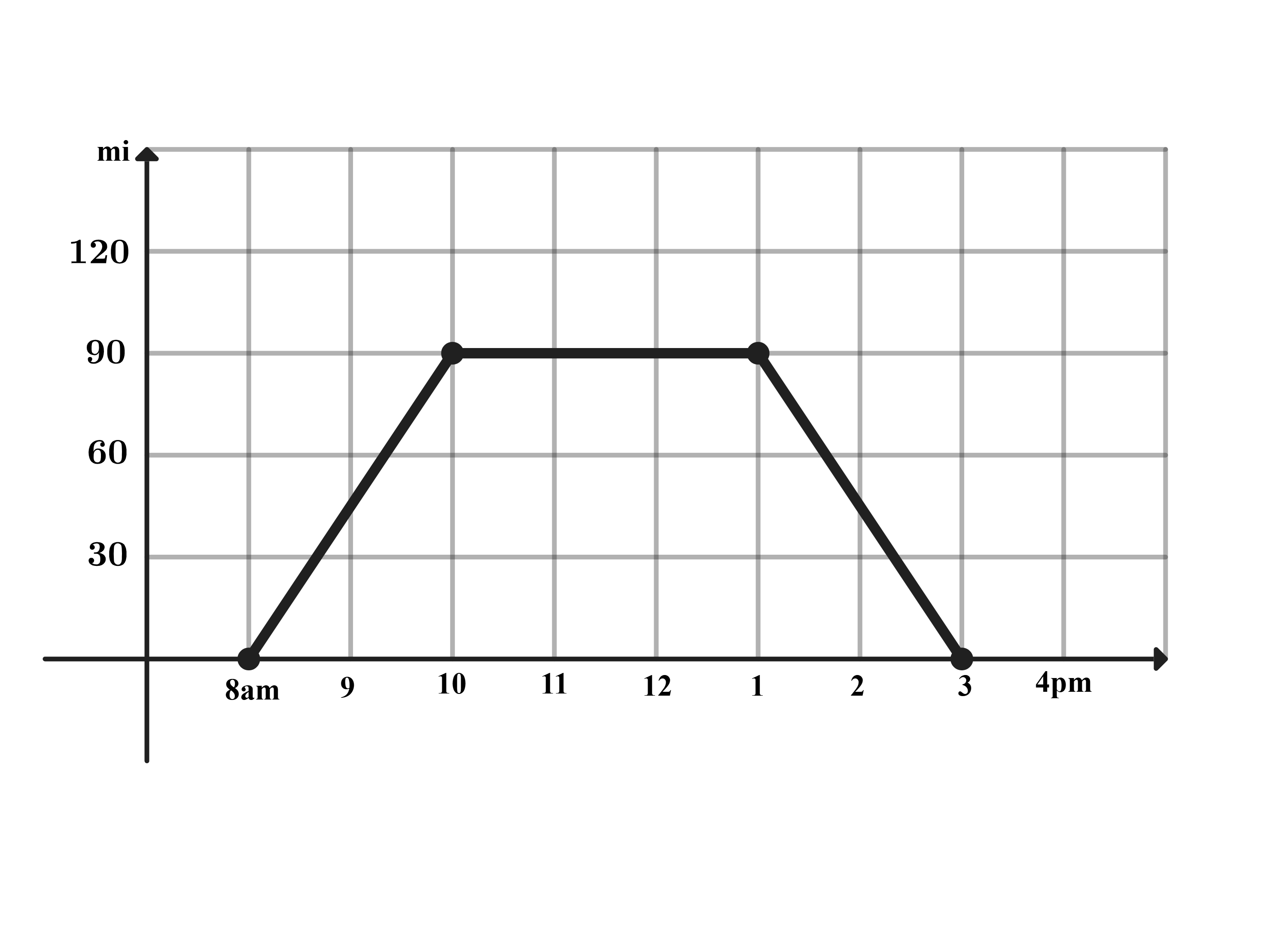
B. 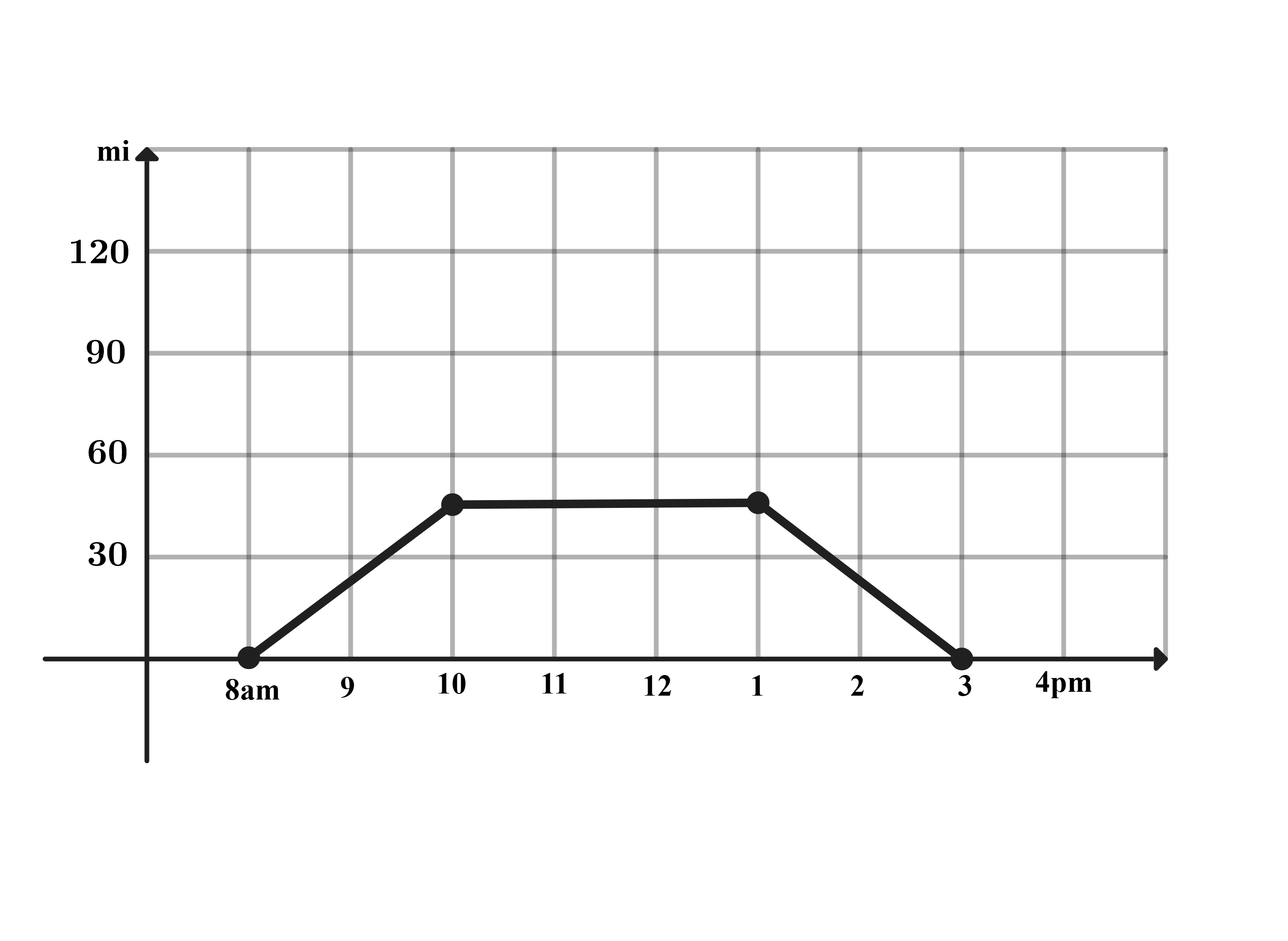
C. 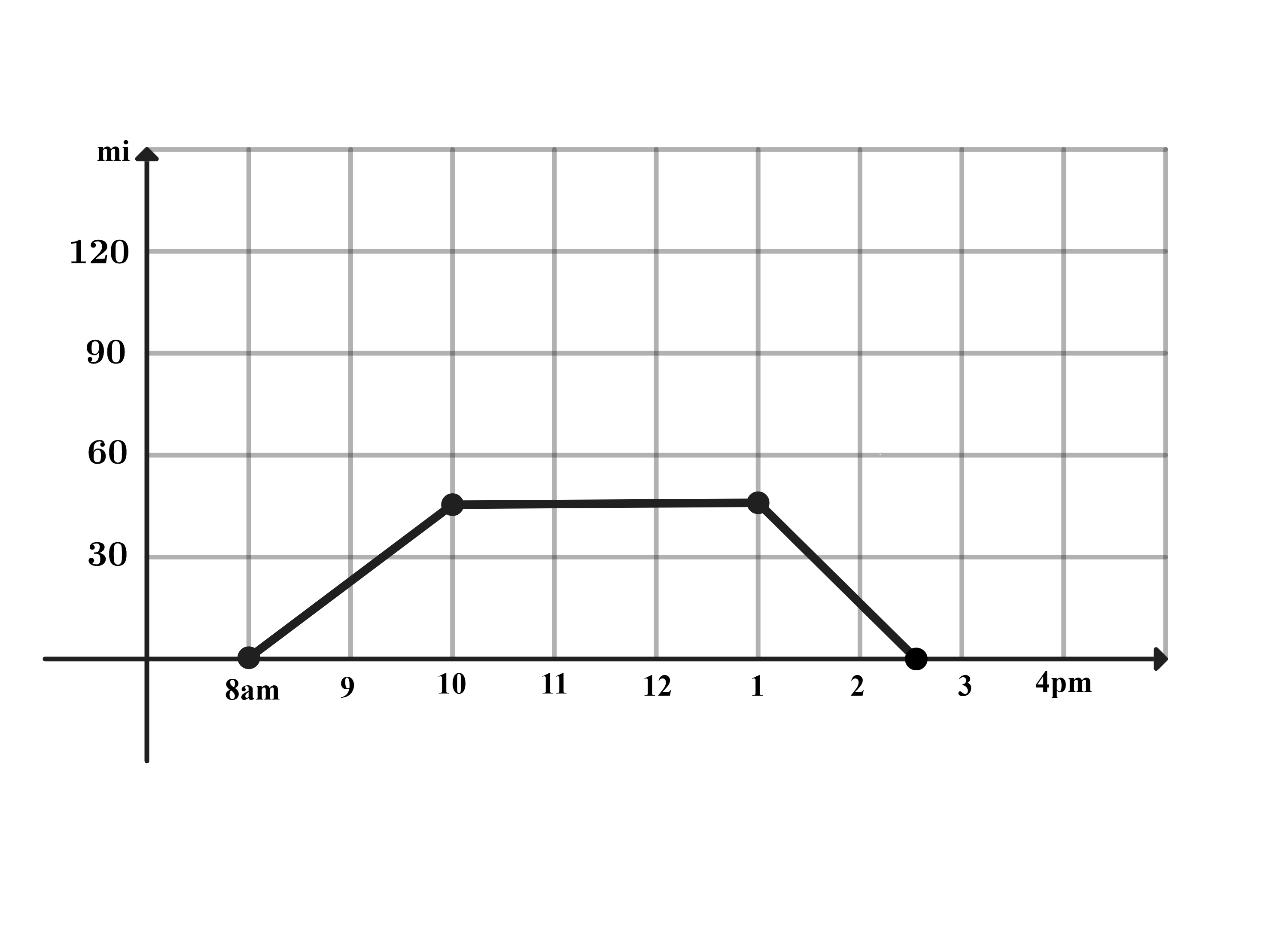
D. 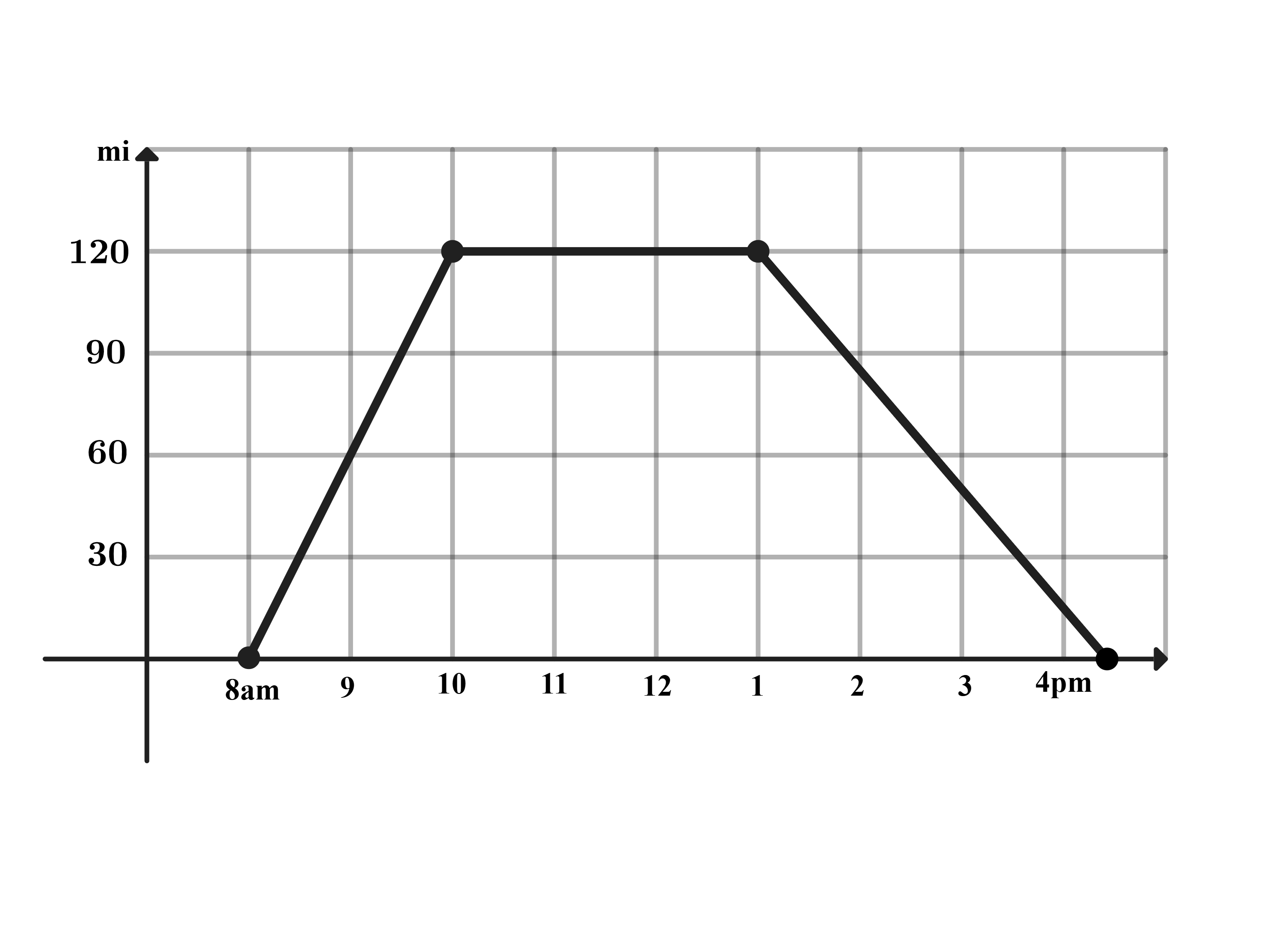
E. 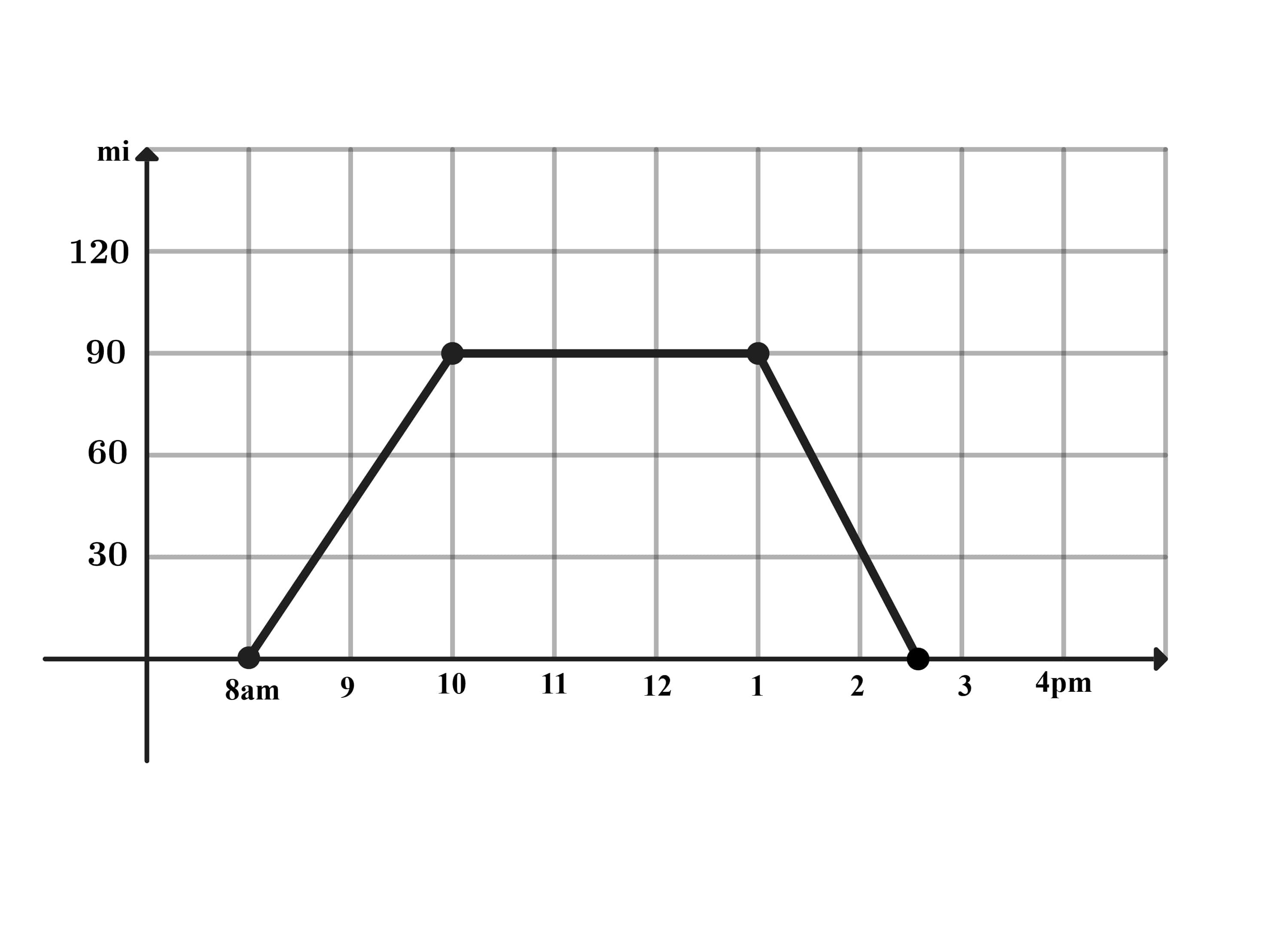
Solution:
Problem 11: Henry the donkey has a very long piece of pasta. He takes a number of bites of pasta, each time eating inches of pasta from the middle of one piece. In the end, he has pieces of pasta whose total length is inches.What is the length, in inches, of the piece of pasta he started with?
Answer Choices:
A.
B.
C.
E.
Solution:
Problem 12: The arrows on the two spinners shown below are spun. Let the number equal times the number on Spinner , added to the number on Spinner . What is the probability that is a perfect square number?
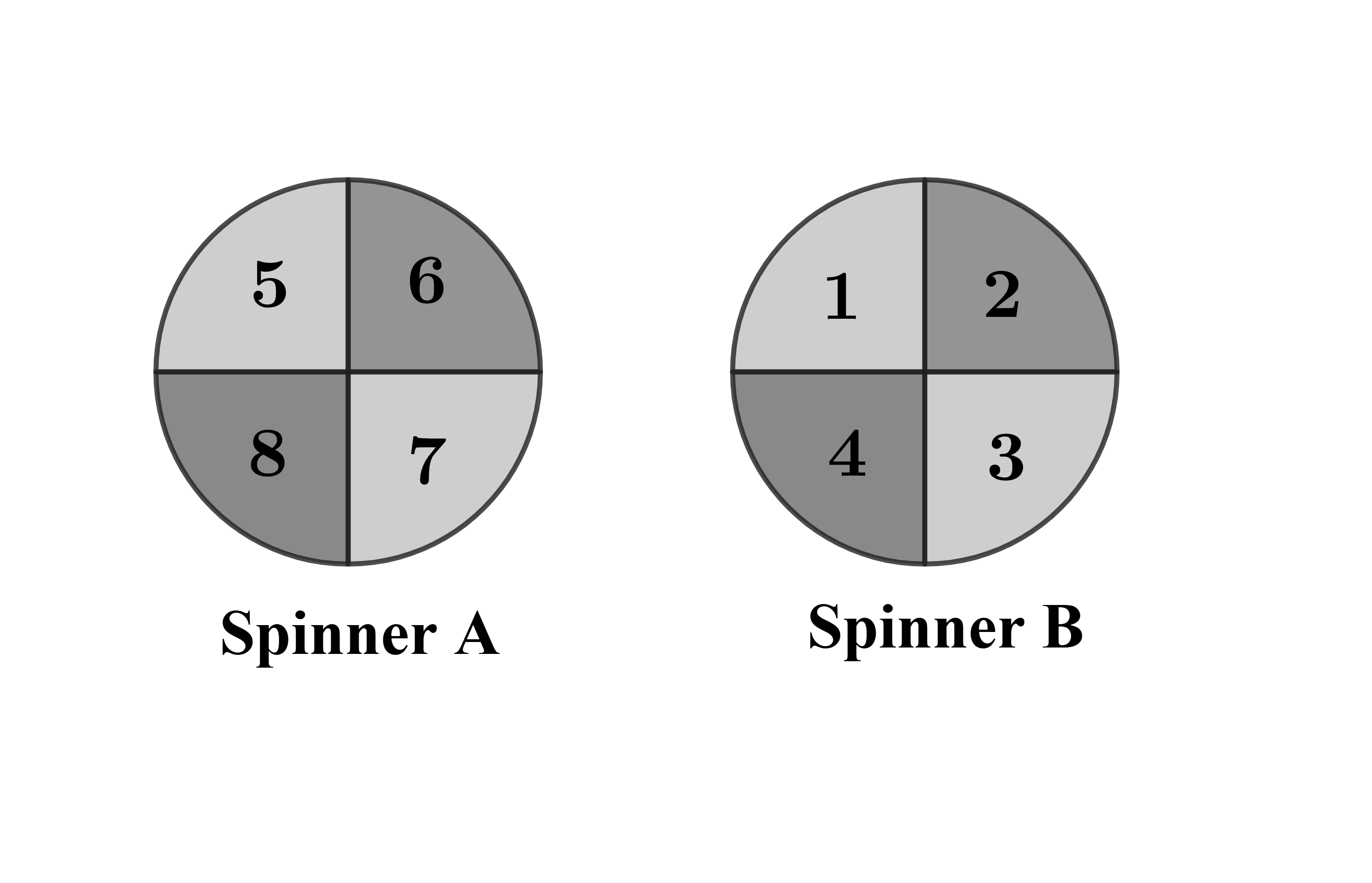
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many positive integers can fill the blank in the sentence below? “One positive integer is more than twice another, and the sum of the two numbers is .”
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: In how many ways can the letters in be rearranged so that two or more E's do not appear together?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: László went online to shop for black pepper and found thirty different black pepper options varying in weight and price, shown in the scatter plot below. In ounces, what is the weight of the pepper that offers the lowest price per ounce?
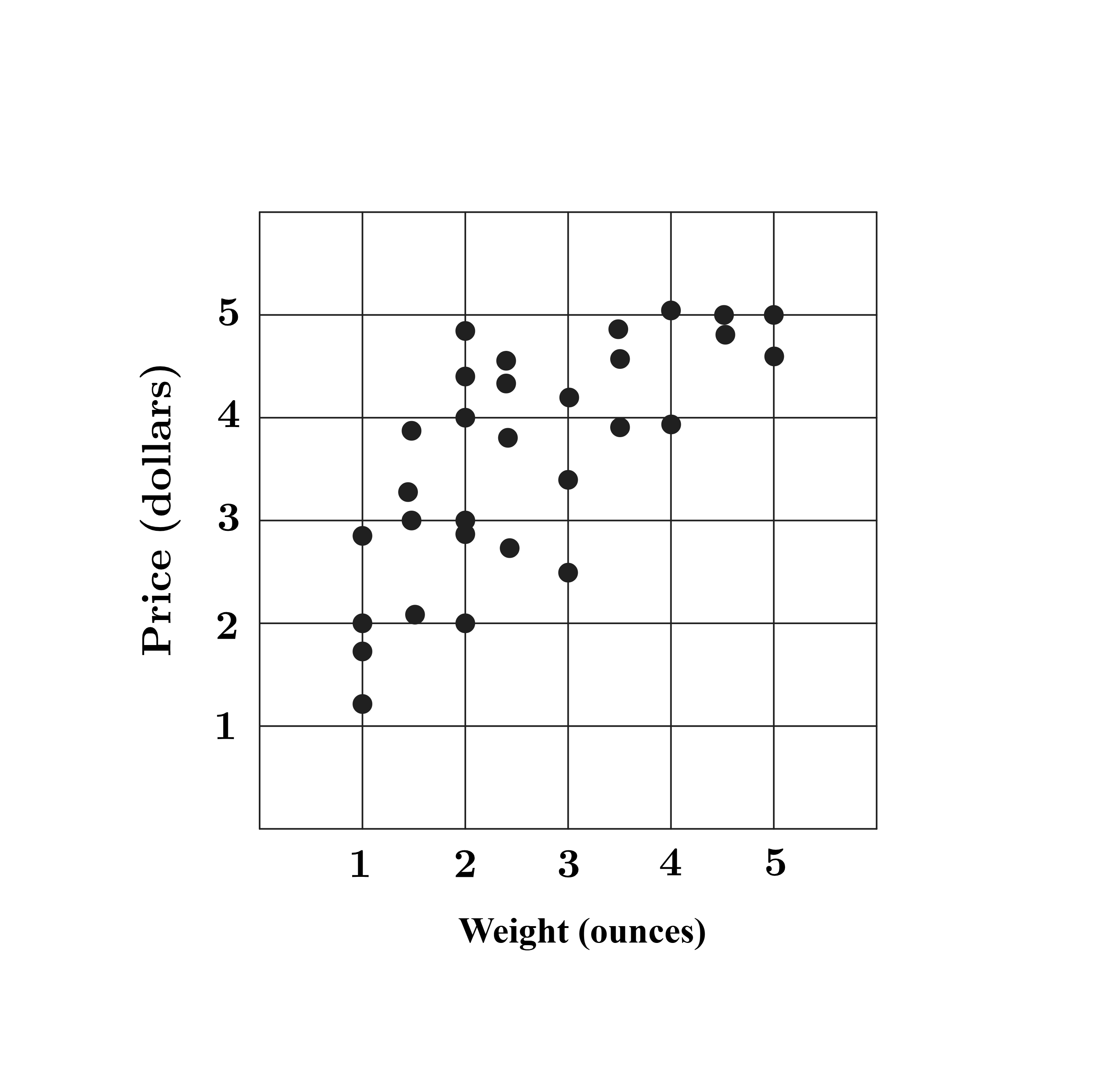
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Four numbers are written in a row. The average of the first two is , the average of the middle two is , and the average of the last two is . What is the average of the first and last of the numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If is an even positive integer, the double factorial notation represents the product of all the even integers from to . For example:
What is the units digit of the following sum?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The midpoints of the four sides of a rectangle are:
What is the area of the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Mr. Ramos gave a test to his class of students. The dot plot below shows the distribution of test scores.
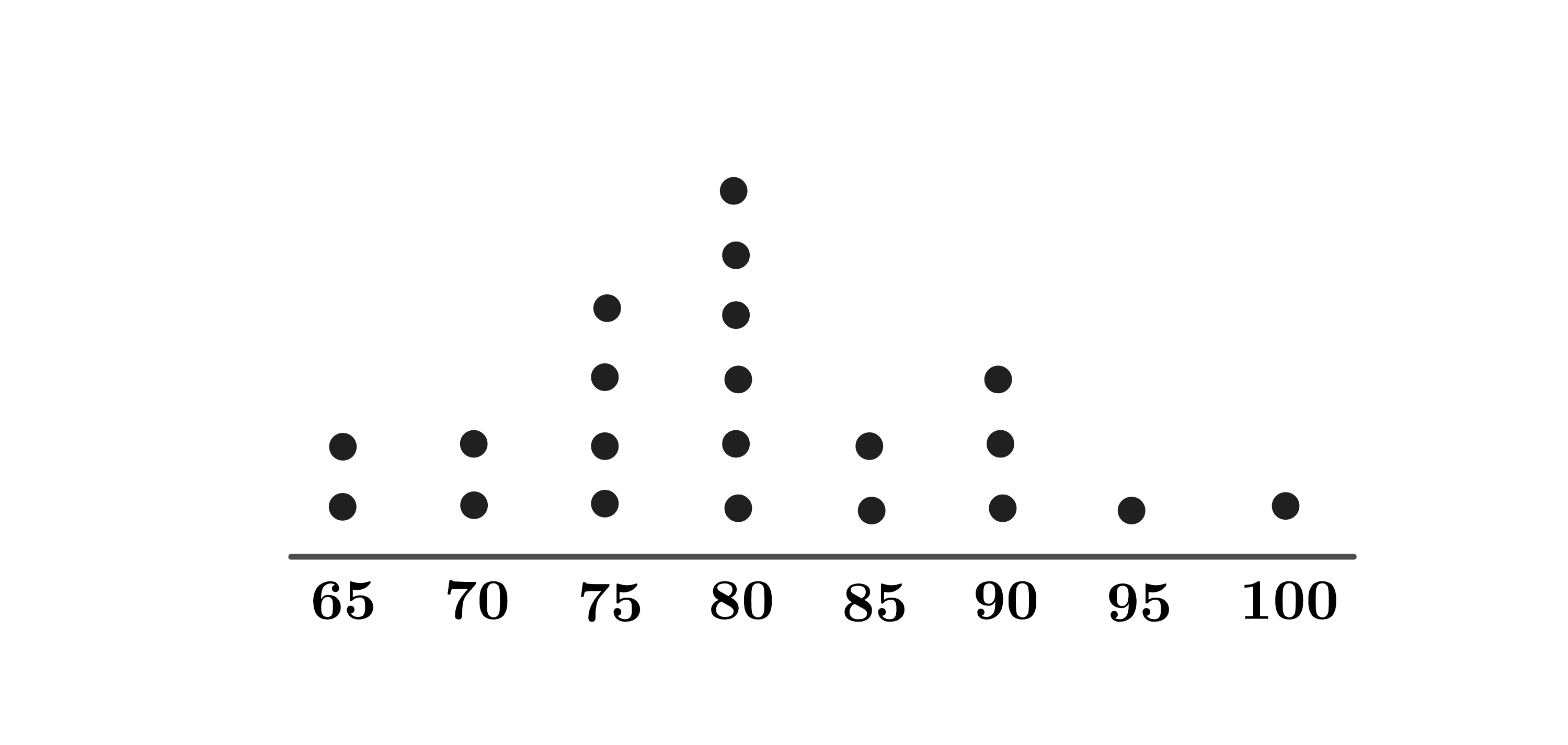
Later Mr. Ramos discovered that there was a scoring error on one of the questions. He regraded the tests, awarding some of the students extra points, which increased the median test score to . What is the minimum number of students who received extra points? (Note that the median test score equals the average of the scores in the middle if the test scores are arranged in increasing order.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The grid below is to be filled with integers in such a way that the sum of the numbers in each row and the sum of the numbers in each column are the same. Four numbers are missing. The number in the lower left corner is larger than the other three missing numbers. What is the smallest possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Steph scored baskets out of attempts in the first half of a game, and baskets out of attempts in the second half. Candace took attempts in the first half and attempts in the second. In each half, Steph scored a higher percentage of baskets than Candace. Surprisingly they ended with the same overall percentage of baskets scored. How many more baskets did Candace score in the second half than in the first?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A bus takes minutes to drive from one stop to the next, and waits minute at each stop to let passengers board. Zia takes minutes to walk from one bus stop to the next. As Zia reaches a bus stop, if the bus is at the previous stop or has already left the previous stop, then she will wait for the bus. Otherwise she will start walking toward the next stop. Suppose the bus and Zia start at the same time toward the library, with the bus stops behind. After how many minutes will Zia board the bus?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A or is placed in each of the nine squares in a grid. Shown below is a sample configuration with three 's in a line.
How many configurations will have three 's in a line and three 's in a line? To determine the number of configurations with three 's in a line and three 's in a line?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The figure below shows a polygon , consisting of rectangles and right triangles. When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that and . What is the volume of the prism?
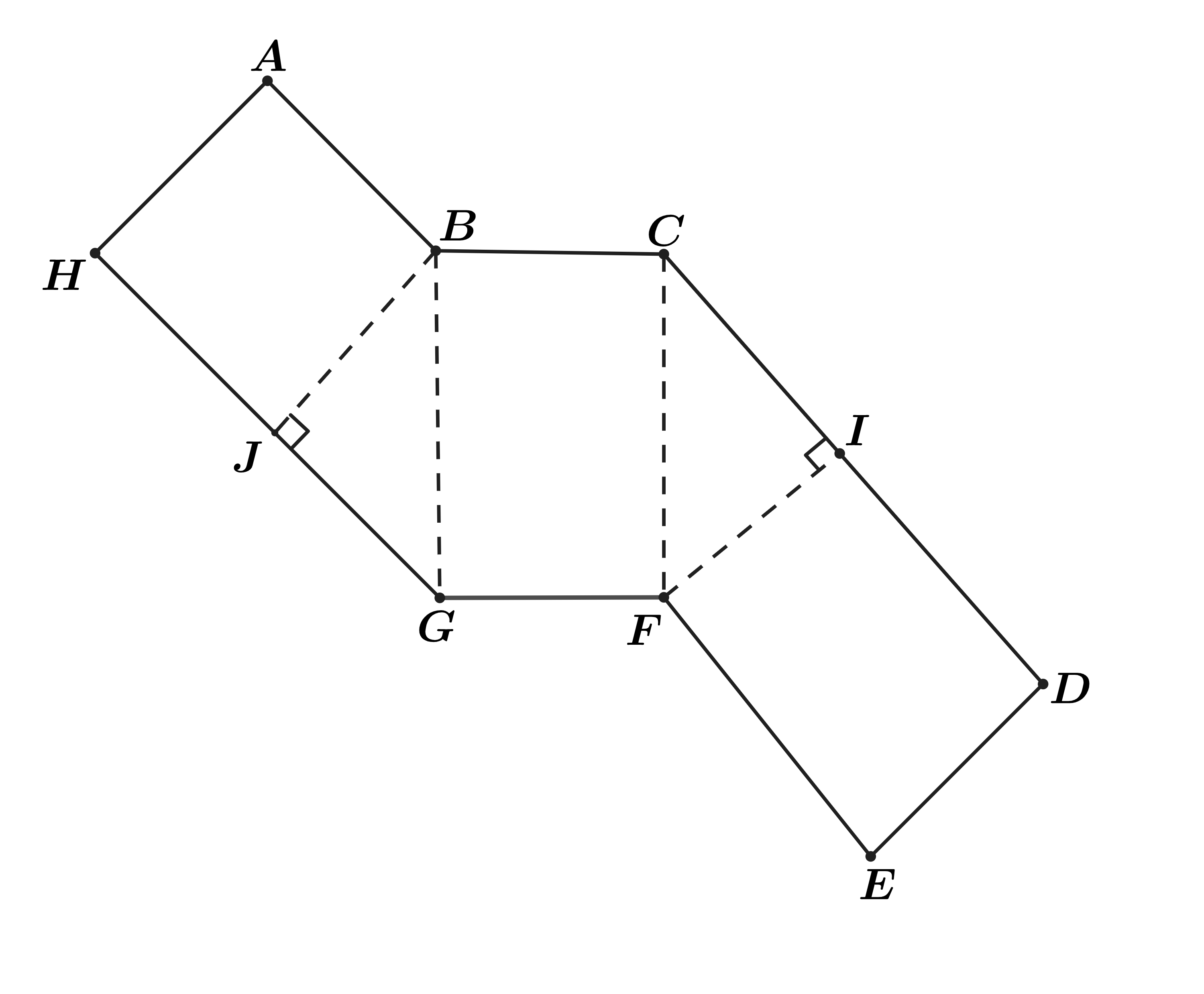
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A cricket randomly hops between leaves, on each turn hopping to one of the other leaves with equal probability. After hops, what is the probability that the cricket has returned to the leaf where it started?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions