¶ 2019 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2019 AIME II problems here.
Discussion Forum
Engage in discussion about the 2019 AIME II math contest by visiting Random Math AIME II 2019 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2019 AIME II problems, please refer below:
Problem 1: Points lie on the same side of line so that and are congruent with , and . The intersection of these two triangular regions has area , where and are relatively prime positive integers. Find .
Solution:
Problem 2: Lily pads lie in a row on a pond. A frog makes a sequence of jumps starting on pad . From any pad the frog jumps to either pad or pad chosen randomly and independently with probability . The probability that the frog visits pad is , where and are relatively prime positive integers. Find .
Solution:
Problem 3: Find the number of -tuples of positive integers that satisfy the following systems of equations:
Solution:
Problem 4: A standard six-sided fair die is rolled four times. The probability that the product of all four numbers rolled is a perfect square is , where and are relatively prime positive integers. Find .
Solution:
Problem 5: Four ambassadors and one advisor for each of them are to be seated at a round table chairs numbered in order from to . Each ambassador must sit in an even-numbered chair. Each advisor must sit in a chair adjacent to his or her ambassador. There are ways for the people to be seated at the table under these conditions. Find the remainder when is divided by .
Solution:
Problem 6: In a Martian civilization, all logarithms whose bases are not specified are assumed to be base , for some fixed . A Martian student writes down
and finds that this system of equations has a single real number solution . Find .
Solution:
Problem 7: Triangle has side lengths , and . Lines , and are drawn parallel to , and , respectively, such that the intersection of , and with the interior of are segments of length , and , respectively. Find the perimeter of the triangle whose sides lie on , and .
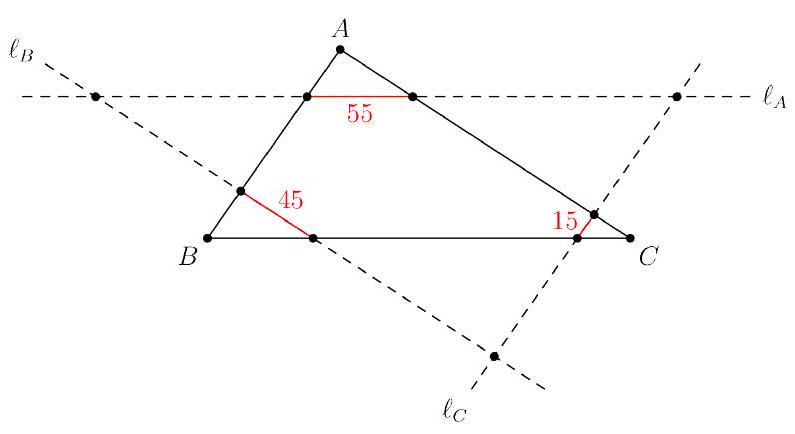
Solution:
Problem 8: The polynomial has real coefficients not exceeding , and . Find the remainder when is divided by .
Solution:
Problem 9: Call a positive integer -pretty if has exactly positive divisors and is divisible by . For example, is -pretty. Let be the sum of positive integers less than that are -pretty. Find .
Solution:
Problem 10: There is a unique angle between and such that for nonnegative integers , the value of is positive when is a multiple of , and negative otherwise. The degree measure of is , where and are relatively prime integers. Find .
Solution:
Problem 11: Triangle has side lengths , and . Circle passes through and is tangent to line at . Circle passes through and is tangent to line at . Let be the intersection of circles and not equal to . Then , where and are relatively prime positive integers. Find .
Solution:
Problem 12: For call a finite sequence of positive integers progressive if and divides for all . Find the number of progressive sequences such that the sum of the terms in the sequence is equal to .
Solution:
Problem 13: Regular octagon is inscribed in a circle of area . Point lies inside the circle so that the region bounded by , and the minor arc of the circle has area , while the region bounded by , and the minor arc of the circle has area . There is a positive integer such that the area of the region bounded by , and the minor arc is equal to . Find .
Solution:
Problem 14: Find the sum of all positive integers such that, given an unlimited supply of stamps of denominations , and cents, cents is the greatest postage that cannot be formed.
Solution:
Problem 15: In acute triangle points and are the feet of the perpendiculars from to and from to , respectively. Line intersects the circumcircle of in two distinct points, and . Suppose , and . The value of can be written in the form where and are positive integers, and is not divisible by the square of any prime. Find .
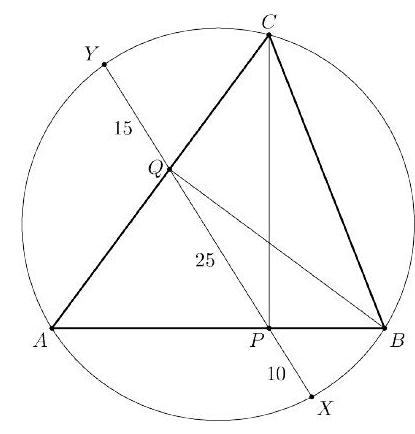
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions