¶ 2012 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2012 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2012 AMC8 math contest by visiting Random Math 2012 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2012 AMC8 problems, please refer below:
Problem 1: Rachelle uses pounds of meat to make hamburgers for her family. How many pounds of meat does she need to make hamburgers for a neighborhood picnic?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: In the county of East Westmore, statisticians estimate there is a baby born every hours and a death every day. To the nearest hundred, how many people are added to the population of East Westmore each year?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: On February The Oshkosh Northwester listed the length of daylight as hours and minutes, the sunrise as AM, and the sunset as PM. The length of daylight and sunrise were correct, but the sunset was wrong. When did the sun really set?
.jpg)
Answer Choices:
A. PM
B. PM
C. PM
D. PM
E. PM
Solution:
Problem 4: Peter's family ordered a -slice pizza for dinner. Peter ate one slice and shared another slice equally with his brother Paul. What fraction of the pizza did Peter eat?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In the diagram, all angles are right angles and the lengths of the sides are given in centimeters. Note the diagram is not drawn to scale. What is , in centimeters?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A rectangular photograph is placed in a frame that forms a border two inches wide on all sides of the photograph. The photograph measures inches high and inches wide. What is the area of the border, in square inches?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Isabella must take four -point tests in her math class. Her goal is to achieve an average grade of at least on the tests. Her first two test scores were and . After seeing her score on the third test, she realized that she could still reach her goal. What is the lowest possible score she could have made on the third test?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A shop advertises that everything is "half price in today's sale." In addition, a coupon gives a discount on sale prices. Using the coupon, the price today represents what percentage discount off the original price?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The Fort Worth Zoo has a number of two-legged birds and a number of fourlegged mammals. On one visit to the zoo, Margie counted heads and legs. How many of the animals that Margie counted were two-legged birds?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: How many -digit numbers greater than are there that use the four digits of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The mean, median, and unique mode of the positive integers are all equal. What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: What is the units digit of .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Jamar bought some pencils costing more than a penny each at the school bookstore and paid . Sharona bought some of the same pencils and paid . How many more pencils did Sharona buy than Jamar?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: In the BIG N, a middle school football conference, each team plays every other team exactly once. If a total of conference games were played during the season, how many teams were members of the BIG N conference?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The smallest number greater than that leaves a remainder of when divided by , or lies between what numbers?
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 16: Each of the digits , and is used only once to make two five-digit numbers so that they have the largest possible sum. Which of the following could be one of the numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A square with an integer side length is cut into squares, all of which have integer side length and at least of which have area . What is the smallest possible value of the length of the side of the original square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: What is the smallest positive integer that is neither prime nor square and that has no prime factor less than
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In a jar of red, green, and blue marbles, all but are red marbles, all but are green, and all but are blue. How many marbles are in the jar?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: What is the correct ordering of the three numbers , and , in increasing order?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Marla has a large white cube that has an edge of feet. She also has enough green paint to cover square feet. Marla uses all the paint to create a white square centered on each face, surrounded by a green border. What is the area of one of the white squares, in square feet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be a set of nine distinct integers. Six of the elements of the set are , and . What is the number of possible values of the median of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: An equilateral triangle and a regular hexagon have equal perimeters. If the area of the triangle is , what is the area of the hexagon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A circle of radius is cut into four congruent arcs. The four arcs are joined to form the star figure shown. What is the ratio of the area of the star figure to the area of the original circle?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A square with area is inscribed in a square with area , with one vertex of the smaller square on each side of the larger square. A vertex of the smaller square divides a side of the larger square into two segments, one of length and the other of length . What is the value of
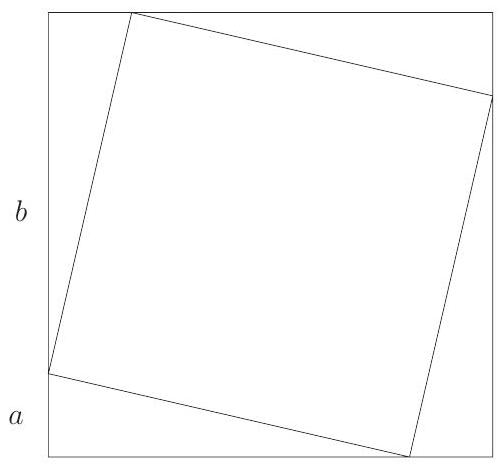
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions