¶ 1952 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1952 AHSME problems, please refer below:
Problem 1: If the radius of a circle is a rational number, its area is given by a number which is:
Answer Choices:
A. (rational)
B. (irrational)
C. (integral)
D. (a perfect square)
E. (none of these)
Solution:
Problem 2: Two high school classes take the same test. One class of 20 students made an average grade of ; the other class of 30 students made an average grade of 70%. The average grade for all students in both classes is:
Answer Choices:
A.
B.
C.
D.
E. (none of these)
Solution:
Problem 3: The expression equals:
Answer Choices:
A.
B.
C.
D.
E. (none of these)
Solution:
Problem 4: The cost of sending a parcel post package weighing pounds, an integer, is 10 cents for the first pound and 3 cents for each additional pound. The formula for the cost is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The points and are connected by a straight line. Another point on this line is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The difference of the roots of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: When simplified, is equal to:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Two equal circles in the same plane cannot have the following number of common tangents:
Answer Choices:
A.
B.
C.
D.
E. (none of these)
Solution:
Problem 9: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: An automobile went up a hill at a speed of 10 miles an hour and down the same distance at a speed of 20 miles an hour. The average speed for the round trip was:
Answer Choices:
A. mph
B. mph
C. mph
D. mph
E. (none of these)
Solution:
Problem 11: If , then it is incorrect to say:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The sum to infinity of the terms of an infinite geometric progression is 6 . The sum of the first two terms is . The first term of the progression is:
Answer Choices:
A. or
B.
C.
D.
E. or
Solution:
Problem 13: The function with and greater than zero has its minimum value when:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A house and store were sold for each. The house was sold at a loss of of the cost, and the store at a gain of of the cost. The entire transaction resulted in:
Answer Choices:
A. no loss or gain
B. loss of
C. gain of
D. gain of
E. (none of these)
Solution:
Problem 15: The sides of a triangle are in the ratio . Then:
Answer Choices:
A. the triangle is obtuse
B. the angles are in the ratio
C. the triangle is acute
D. the angle opposite the largest side is double the angle opposite the smallest side
E. (none of these)
Solution:
Problem 16: If the base of a rectangle is increased by and the area is unchanged, then the altitude is decreased by:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A merchant bought some goods at a discount of off the list price. He wants to mark them at such a price that he can give a discount of of the marked price and still make a profit of of the selling price. The per cent of the list price at which he should mark them is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: only if:
Answer Choices:
A. zero
B.
C.
D.
E.
Solution:
Problem 19: Angle of triangle is trisected by and which meet at and respectively. Then:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If , then the incorrect expression in the following is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The sides of a regular polygon of sides, , are extended to form a star. The number of degrees at each point of the star is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: On hypotenuse of a right triangle a second right triangle is constructed with hypotenuse . If , and , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If has roots which are numerically equal but of opposite signs, the value of must be:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: In the figure, it is given that angle , , and . The area of quadrilateral is:
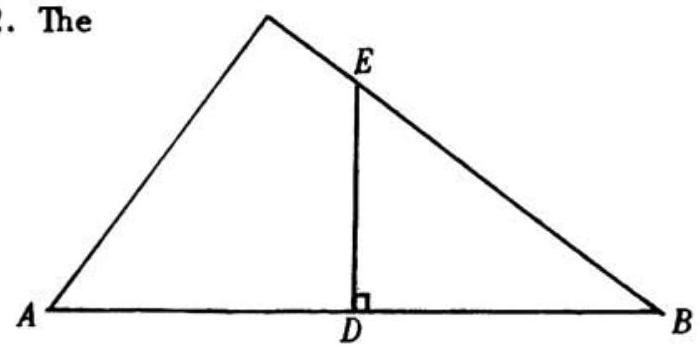
Answer Choices:
A.
B.
C.
D.
E. (none of these)
Solution:
Problem 25: A powderman set a fuse for a blast to take place in 30 seconds. He ran away at a rate of 8 yards per second. Sound travels at the rate of 1080 feet per second. When the powderman heard the blast, he had run approximately:
Answer Choices:
A. yd
B. yd
C. yd
D. yd
E. yd
Solution:
Problem 26: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: The ratio of the perimeter of an equilateral triangle having an altitude equal to the radius of a circle, to the perimeter of an equilateral triangle inscribed in the circle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: In the table shown, the formula relating and is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 29: In a circle of radius 5 units, and are perpendicular diameters. A chord cutting at is 8 units long. The diameter is divided into two segments whose dimensions are:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 30: When the sum of the first ten terms of an arithmetic progression is four times the sum of the first five terms, the ratio of the first term to the common difference is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 31: Given 12 points in a plane no three of which are collinear, the number of lines they determine is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 32: takes 30 minutes less time than to travel a distance of 30 miles. travels mile per hour faster than . If is 's rate of speed in miles per hour, then 's time for the distance is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: A circle and a square have the same perimeter. Then:
Answer Choices:
A. their areas are equal
B. the area of the circle is the greater
C. the area of the square is the greater
D. the area of the circle is times the area of the square
E. none of these
Solution:
Problem 34: The price of an article was increased . Later the new price was decreased . If the last price was one dollar, the original price was:
Answer Choices:
A.
B.
C. one dollar
D.
E.
Solution:
Problem 35: When written with a rational denominator, the expression is equivalent to:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 36: To be continuous at , the value of is taken to be:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 37: Two equal parallel chords are drawn 8 inches apart in a circle of radius 8 inches. The area of that part of the circle that lies between the chords is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 38: The area of a trapezoidal field is 1400 square yards. Its altitude is 50 yards. Find the two bases, if the number of yards in each base is an integer divisible by 8. The number of solutions to this problem is:
Answer Choices:
A. none
B. one
C. two
D. three
E. more than three
Solution:
Problem 39: If the perimeter of a rectangle is and its diagonal is , the difference between the length and width of the rectangle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 40: In order to draw a graph of , a table of values was constructed. These values of the function for a set of equally spaced increasing values of were , and 4761. The one which is incorrect is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 41: Increasing the radius of a cylinder by 6 units increases the volume by cubic units. Increasing the altitude of the cylinder by 6 units also increases the volume by cubic units. If the original altitude is 2, then the original radius is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 42: Let represent a repeating decimal. If denotes the figures of which do not repeat themselves, and denotes the figures which do repeat themselves, then the incorrect expression is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 43: The diameter of a circle is divided into equal parts. On each part a semicircle is constructed. As becomes very large, the sum of the lengths of the arcs of the semi-circles approaches:
Answer Choices:
A. equal to the semi-circumference of the original circle
B. equal to the diameter of the original circle
C. greater than the diameter but less than the semi-circumference of the original circle
D. infinite in length
E. greater than the semi-circumference but finite
Solution:
Problem 44: If an integer of two digits is times the sum of its digits, the number formed by interchanging the digits is the sum of the digits multiplied by:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 45: If and are two unequal positive numbers, then:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 46: The base of a new rectangle equals the sum of the diagonal and the greater side of a given rectangle, while the altitude of the new rectangle equals the difference of the diagonal and the greater side of the given rectangle. The area of the new rectangle is:
Answer Choices:
A. greater than the area of the given rectangle
B. equal to the area of the given rectangle
C. equal to the area of a square with its side equal to the smaller side of the given rectangle
D. equal to the area of a square with its side equal to the greater side of the given rectangle
E. equal to the area of a rectangle whose dimensions are the diagonal and shorter side of the given rectangle
Solution:
Problem 47: In the set of equations , the integral roots in the order are:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 48: Two cyclists, miles apart, and starting at the same time, would be together in hours if they traveled in the same direction, but would pass each other in hours if they traveled in opposite directions. The ratio of the speed of the faster cyclist to that of the slower is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 49: In the figure, and are one-third of their respective sides. It follows that , and similarly for lines and . Then the area of triangle is:
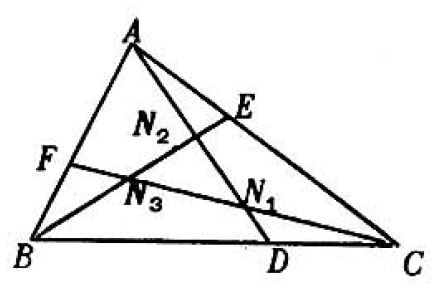
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 50: A line initially 1 inch long, grows according to the following law, where the first term is the initial length.
If the growth process continued forever, the limit of the length of the line is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions