¶ 1955 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1955 AHSME problems, please refer below:
Problem 1: Which one of the following is not equivalent to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The smaller angle between the hands of a clock at p.m. is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If each number in a set of ten numbers is increased by 20 , the arithmetic mean (average) of the original ten numbers:
Answer Choices:
A. remains the same
B. is increased by
C. is increased by
D. is increased by
E. is increased by
Solution:
Problem 4: The equality is satisfied by:
Answer Choices:
A. no real values of
B. either or
C. only
D. only
E. only
Solution:
Problem 5: varies inversely as the square of . When . When equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A merchant buys a number of oranges at for cents and an equal number at for cents. To "break even" he must sell all at:
Answer Choices:
A. for cents
B. for cents
C. for cents
D. for cents
E. for cents
Solution:
Problem 7: If a worker receives a 20 per cent cut in wages, he may regain his original pay exactly by obtaining a raise of:
Answer Choices:
A. per cent
B. per cent
C. per cent
D.
E.
Solution:
Problem 8: The graph of :
Answer Choices:
A. is a hyperbola intersecting only the -axis
B. is a hyperbola intersecting only the -axis
C. is a hyperbola intersecting neither axis
D. is a pair of straight lines
E. does not exist
Solution:
Problem 9: A circle is inscribed in a triangle with sides 8,15 , and 17 . The radius of the circle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: How many hours does it take a train traveling at an average rate of 40 mph between stops to travel miles if it makes stops of minutes each?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The negation of the statement "No slow learners attend this school" is:
Answer Choices:
A. All slow learners attend this school
B. All slow learners do not attend this school
C. Some slow learners attend this school
D. Some slow learners do not attend this school
E. No slow learners do not attend this school
Solution:
Problem 12: The solution of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The fraction is equal to:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The length of rectangle is 10 per cent more than the side of square . The width of the rectangle is 10 per cent less than the side of the square. The ratio of the areas, , is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The ratio of the areas of two concentric circles is . If the radius of the smaller is , then the difference between the radii is best approximated by:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The value of when and is:
Answer Choices:
A.
B.
C.
D. any finite number
E. meaningless
Solution:
Problem 17: If , then equals:
Answer Choices:
A.
B.
C.
D.
E. either or
Solution:
Problem 18: The discriminant of the equation is zero. Hence, its roots are:
Answer Choices:
A. real and equal
B. rational and equal
C. rational and unequal
D. irrational and unequal
E. imaginary
Solution:
Problem 19: Two numbers whose sum is 6 and the absolute value of whose difference is 8 are roots of the equation:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The expression equals zero for:
Answer Choices:
A. no real or imaginary values of
B. no real values of only
C. no imaginary values of only
D.
E.
Solution:
Problem 21: Represent the hypotenuse of a right triangle by and the area by . The altitude on the hypotenuse is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: On a order a merchant has a choice between three successive discounts of , and and three successive discounts of , and . By choosing the better offer, he can save:
Answer Choices:
A. nothing at all
B.
C.
D.
E.
Solution:
Problem 23: In checking the petty cash a clerk counts quarters, dimes, nickels, and cents. Later he discovers that of the nickels were counted as quarters and of the dimes were counted as cents. To correct the total obtained the clerk must:
Answer Choices:
A. make no correction
B. subtract cents
C. subtract cents
D. add cents
E. add cents
Solution:
Problem 24: The function :
Answer Choices:
A. always increases as increases
B. always decreases as decreases to
C. cannot equal
D. has a maximum value when is negative
E. has a minimum value of
Solution:
Problem 25: One of the factors of is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 26: Mr. A owns a house worth . He sells it to Mr. B at profit. Mr. B sells the house back to Mr. A at a loss. Then:
Answer Choices:
A. Mr. A comes out even
B. Mr. A makes
C. Mr. A makes
D. Mr. B loses
E. none of the above is correct
Solution:
Problem 27: If and are the roots of , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: On the same set of axes are drawn the graph of and the graph of the equation obtained by replacing by in the given equation. If and these two graphs intersect:
Answer Choices:
A. in two points, one on the -axis and one on the -axis
B. in one point located on neither axis
C. only at the origin
D. in one point on the -axis
E. in one point on the -axis
Solution:
Problem 29: In the figure is tangent to semicircle is tangent to semicircle is a straight line; the arcs are indicated in the figure. Angle is measured by:
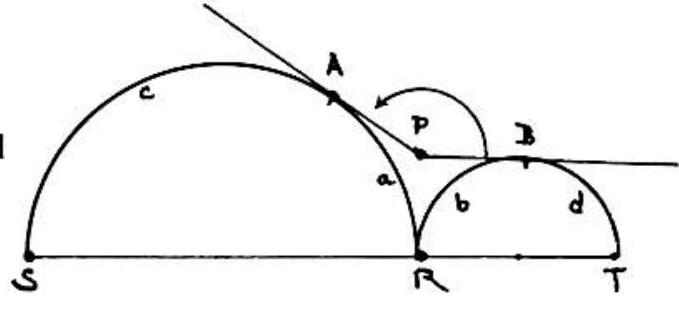
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Each of the equations has:
Answer Choices:
A. two integral roots
B. no root greater than 3
C. no root zero
D. only one root
E. one negative root and one positive root
Solution:
Problem 31: An equilateral triangle whose side is 2 is divided into a triangle and a trapezoid by a line drawn parallel to one of its sides. If the area of the trapezoid equals one-half of the area of the original triangle, the length of the median of the trapezoid is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: If the discriminant of is zero, then another true statement about , and is that:
Answer Choices:
A. they form an arithmetic progression
B. they form a geometric progression
C. they are unequal
D. they are all negative numbers
E. only is negative and and are positive
Solution:
Problem 33: Henry starts a trip when the hands of the clock are together between 8 a.m. and 9 a.m. He arrives at his destination between . and . when the hands of the clock are exactly apart. The trip takes:
Answer Choices:
A. hr .
B. hr . min.
C. hr . min.
D. hr . min .
E. none of these
Solution:
Problem 34: A 6 -inch and 18 -inch diameter pole are placed as in the figure and bound together with wire. The length of the shortest wire that will go around them is:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: Three boys agree to divide a bag of marbles in the following manner. The first boy takes one more than half the marbles. The second takes a third of the number remaining. The third boy finds that he is left with twice as many marbles as the second boy. The original number of marbles.
Answer Choices:
A. none of these answers
B. cannot be determined from the given data
C. or
D. or
E. or
Solution:
Problem 36: A cylindrical oil tank, lying horizontally, has an interior length of 10 feet and an interior diameter of 6 feet. If the rectangular surface of the oil has an area of 40 square feet, the depth of the oil is.
Answer Choices:
A.
B.
C.
D.
E. either or
Solution:
Problem 37: A three-digit number has, from left to right, the digits , and with . When the number with the digits reversed is subtracted from the original number, the units' digit in the difference is 4 . The next two digits, from right to left, are.
Answer Choices:
A. and
B. and
C. impossible to tell
D. and
E. and
Solution:
Problem 38: Four positive integers are given. Select any three of these integers, find their arithmetic average, and add this result to the fourth integer. Thus the numbers and 17 are obtained. One of the original integers is.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 39: If , then if the least possible value of is zero is equal to.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 40: The fractions and are unequal if.
Answer Choices:
A. and
B.
C.
D.
E.
Solution:
Problem 41: A train traveling from Aytown to Beetown meets with an accident after l hr. It is stopped for ., after which it proceeds at four-fifths of its usual rate, arriving at Beetown 2 hr . late. If the train had covered 80 miles more before the accident, it would have been just 1 hr . late. The usual rate of the train is.
Answer Choices:
A. 20 mph
B. 30 mph
C. 40 mph
D. 50 mph
E. 60 mph
Solution:
Problem 42: If , and are positive integers, the radicals and are equal when and only when.
Answer Choices:
A.
B. and
C.
D. and is any value
E. and
Solution:
Problem 43: The pairs of values of and that are the cormon solutions of the equations and are.
Answer Choices:
A. 3 real pairs
B. 4 real pairs
C. 4 imaginary pairs
D. 2 real and 2 imaginary pairs
E. 1 real and 2 imaginary pairs
Solution:
Problem 44: In circle chord is produced so that equals a radius of the circle. -is drawn and extended to . is drawn. Which of the following expresses the relationship between and ?
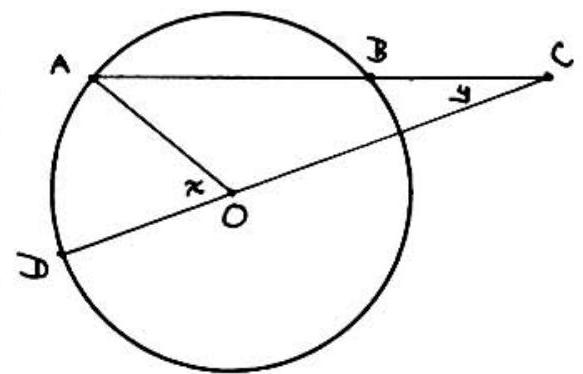
Answer Choices:
A.
B.
C.
D. there is no special relationship between and
E. or , depending upon the length of
Solution:
Problem 45: Given a geometric sequence with the first term and and an arithmetic sequence with the first term . A third sequence is formed by adding corresponding terms of the two given sequences. The sum of the first ten terms of the third sequence is.
Answer Choices:
A.
B.
C.
D.
E. not possible to determine from the information given.
Solution:
Problem 46: The graphs of , and intersect in.
Answer Choices:
A. 6 points
B. 1 point
C. 2 points
D. no points
E. an unlimited number of points
Solution:
Problem 47: The expressions and are.
Answer Choices:
A. always equal
B. never equal
C. equal whenever
D. equal when
E. equal only when
Solution:
Problem 48: Given triangle with medians parallel and equal to and are drawn; extended meets in . Which one of the following statements is not necessarily correct?
.jpg)
Answer Choices:
A. is a parallelogram
B.
C.
D.
E. is a median of triangle
Solution:
Problem 49: The graphs of and intersect in.
Answer Choices:
A. 1 point whose abscissa is 2
B. 1 point whose abscissa is 0
C. no points
D. two distinct points
E. two identical points
Solution:
Problem 50: In order to pass going 40 mph on a two-lane highway , going 50 mph , must gain 30 feet. Meantime, feet from , is headed toward him at 50 mph . If and maintain their speeds, then, in order to pass safely, must increase his speed by.
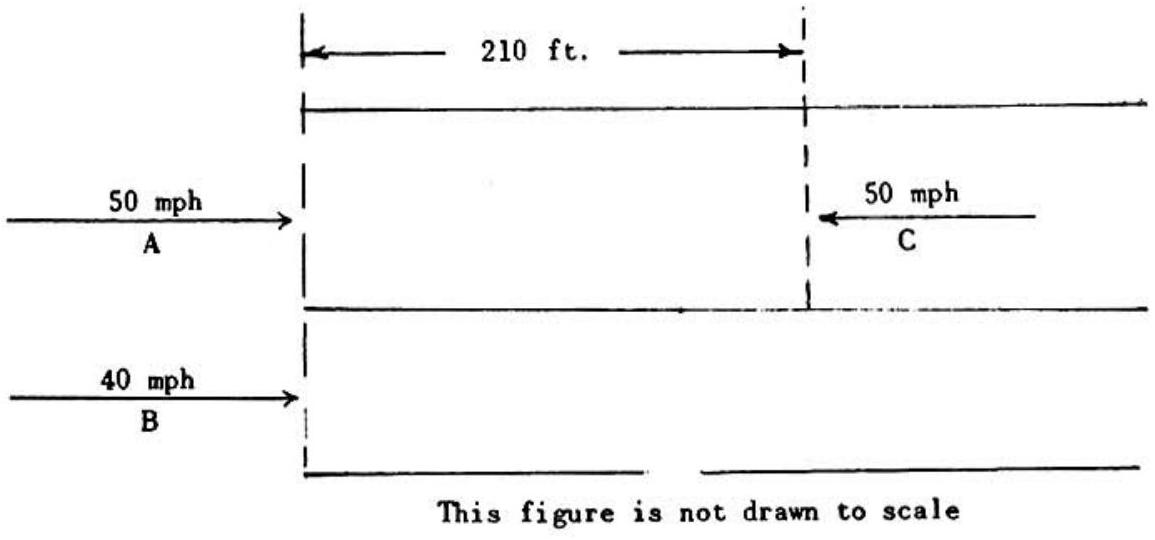
Answer Choices:
A. 30 mph
B. 10 mph
C. 5 mph
D. 15 mph
E. 3 mph
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions