¶ 1968 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1968 AHSME problems, please refer below:
Problem 1: Let units be the increase in the circumference of a circle resulting from an increase of units in the diameter. Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The real value of such that divided by equals is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A straight line passing through the point is perpendicular to the line . Its equation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Define an operation * for positive real numbers as . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Let side of convex quadrilateral be extended through and let side be extended through , to meet in point . Let represent the degree-sum of angles CDE and DCE and let represent the degreesum of angles and . If , then:
Answer Choices:
A. sometimes, sometimes
B. sometimes, sometimes
C.
D.
E.
Solution:
Problem 7: Let be the intersection point of medians and of triangle . If is 3 inches, then , in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A positive number is mistakenly divided by 6 instead of being multiplied by 6. Based on the correct answer, the error thus committed, to the nearest percent, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The sum of the real values of satisfying the equality is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Assume that, for a certain school, it is true that
I: Some students are not honest.
II: All fraternity members are honest.
A necessary conclusion is:
Answer Choices:
A. Some students are fraternity members.
B. Some fraternity members are not students
C. Some students are not fraternity members
D. No fraternity member is a student
E. No student is a fraternity member.
Solution:
Problem 11: If an arc of on circle I has the same length as an arc of on circle II, the ratio of the area of circle to that of circle II is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 12: A circle passes through the vertices of a triangle with side-lengths , . The radius of the circle is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If and are the roots of , then the sum of the roots is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: If and are non-zero numbers such that and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let equal the product of any three consecutive positive odd integers. The largest integer dividing all such is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If is such that and , then:
Answer Choices:
A.
B.
C.
D. or
E. or
Solution:
Problem 17: Let . where is a positive integer. If , the set of possible values of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Side of triangle has length 8 inches. Line is drawn parallel to so that is on segment and is on segment . Line AE extended bisects angle FEC. If DE has length 5 inches, then the length of , in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Let n be the number of ways that 10 dollars can be changed into dimes and quarters, with at least one of each coin being used. Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The measures of the interior angles of a convex polygon of sides are in arithmetic progression. If the common difference is and the largest angle is , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If all the operations in are correctly performed, the units digit in the value of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A segment of length 1 is divided into four segments. Then there exists a simple quadrilateral with the four segments as sides if and only if each segment is:
Answer Choices:
A. equal to
B. equal to or greater than and less than
C. greater than and less than
D. greater than and less than
E. less than
Solution:
Problem 23: If all the logarithms are real numbers, the equality is satisfied for:
Answer Choices:
A. all real values of
B. no real values of
C. all real values of except
D. no real values of except
E. all real values of except
Solution:
Problem 24: A painting is to be placed into a wooden frame with the longer dimension vertical. The wood at the top and bottom is twice as wide as the wood on the sides. If the frame area equals that of the painting itself, the ratio of the smaller to the larger dimension of the framed painting is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Ace runs with constant speed and Flash runs times as fast, . Flash gives Ace a head start of yards, and, at a given signal, they start off in the same direction. Then the number of yards Flash must run to catch Ace is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Let , where is the smallest positive integer such that . Then the sum of the digits of is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Let Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: If the arithmetic mean of and is double their geometric mean, with , then a possible value for the ratio , to the nearest integer, is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 29: Given the three numbers , with . Arranged in order of increasing magnitude, they are:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Convex polygons and are drawn in the same plane with and sides, respectively, . If and do not have any line segment in common, then the maximum number of intersections of and is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 31: In this diagram, not drawn to scale, figures I and III are equilateral triangular regions with respective areas of and , square inches. Figure II is a square region with area 32 sq. in. Let the length of segment AD be decreased by of itself, while the lengths of and remain unchanged. The percent decrease in the area of the square is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: A and B move uniformly along two straight paths intersecting at right angles in point O . When A is at is 500 yards short of O . In 2 minutes they are equidistant from , and in 8 minutes more they are again equidistant from . Then the ratio of A's speed to B's speed is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: A number N has three digits when expressed in base 7. When N is expressed in base 9 the digits are reversed. Then the middle digit is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: With 400 members voting the House of Representatives defeated a bill. A re-vote, with the same members voting, resulted in passage of the bill by twice the margin by which it was originally defeated. The number voting for the bill on the re-vote was of the number voting against it originally. How many more members voted for the bill the second time than voted for it the first time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: In this diagram the center of the circle is , the radius is a inches, chord is parallel to chord are collinear, and is the midpoint of . Let . in.) represent the area of trapezoid and let (sq. in.) represent the area of rectangle . Then as and are translated upward so that increases toward the value of , while always equals , the ratio becomes arbitrarily close to:
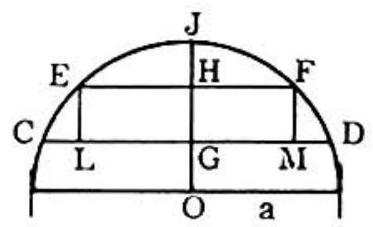
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions