¶ 1969 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1969 AHSME problems, please refer below:
Problem 1: When is added to both the numerator and the denominator of the fraction , the value of the fraction is changed to . Then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If an item is sold for x dollars, there is a loss of based on the cost. If, however, the same item is sold for dollars, there is a profit of based on the cost. The ratio is:
Answer Choices:
A.
B.
C.
D. dependent upon the cost
E. none of these.
Solution:
Problem 3: If N , written in base 2 , is 11000 , the integer immediately preceding N , written in base 2, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let a binary operation on ordered pairs of integers be defined as . Then, if and represent identical pairs, equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If a number , diminished by four times its reciprocal, equals a given real constant , then, for this given , the sum of all such possible values of N is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The area of the ring between two concentric circles is square inches. The length of a chord of the larger circle tangent to the smaller circle, in inches, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If the points and lie on the graph of , and , then equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Triangle ABC is inscribed in a circle. The measures of the nonoverlapping minor , and CA are, respectively, , . Then one interior angle of the triangle, in degrees, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The arithmetic mean (ordinary average) of the fifty-two successive positive integers beginning with 2 , is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The number of points equidistant from a circle and two parallel tangents to the circle, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Given points and in the -plane; point is taken so that is a minimum. Then equals:
Answer Choices:
A.
B.
C.
D.
E. either or .
Solution:
Problem 12: Let be the square of an expression which is linear in x. Then m has a particular value between:
Answer Choices:
A. 3 and 4
B. 4 and 5
C. 5 and 6
D. -4 and -3
E. -6 and -5
Solution:
Problem 13: A circle with radius is contained within the region bounded by a circle with radius . The area bounded by the larger circle is times the area of the region outside the smaller circle and inside the larger circle. Then : equals:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The complete set of -values satisfying the inequality is the set of all such that:
Answer Choices:
A. or or
B. or
C. or
D. or
E. is any real number except 1 or -1
Solution:
Problem 15: In a circle with center at and radius , chord is drawn with length equal to (units). From a perpendicular to meets at . From a perpendicular to meets at . In terms of the area of triangle MDA, in appropriate square units, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: When , is expanded by the binomial theorem, it is found that, when , where k is a positive integer, the sum of the second and third terms is zero. Then equals:
Answer Choices:
A.
B.
C.
D. 2 k
E.
Solution:
Problem 17: The equation is satisfied by:
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 18: The number of points common to the graphs of and is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The number of distinct ordered pairs ( ) where and have positive integral values satisfying the equation is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let equal the product of and . The number of digits in is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If the graph of is tangent to the graph of , then:
Answer Choices:
A. m must equal
B. m must equal
C. must equal
D. m must equal 2
E. m may be any non-negative real number
Solution:
Problem 22: Let be the measure of the area bounded by the -axis, the line , and the curve defined by when when . Then is:
Answer Choices:
A.
B.
C.
D.
E. less than 44 but arbitrarily close to it
Solution:
Problem 23: For the number of prime numbers greater than and less than , is: ; thus:
Answer Choices:
A.
B.
C.
D.
E. for even, for odd
Solution:
Problem 24: When the natural numbers and , with , are divided by the natural number , the remainders are and , respectively. When and are divided by , the remainders are and , respectively. Then:
Answer Choices:
A. always
B. always
C. sometimes and sometimes
D. sometimes and sometimes
E. always
Solution:
Problem 25: If it is known that and that ab is a maximum, then the least value that can be taken on by is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 26: A parabolic arch has a height of 16 inches and a span of 40 inches. The height, in inches, of the arch at a point 5 inches from the center M , is:
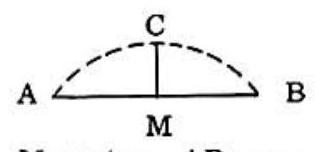
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: A particle moves so that its speed for the second and subsequent miles - varies inversely as the integral number of miles already traveled. For each subsequent mile the speed is constant. If the second mile is traversed in 2 hours, then the time, in hours, needed to traverse the nth mile is:
Answer Choices:
A.
B.
C.
D. 2 n
E.
Solution:
Problem 28: Let n be the number of points P interior to the region bounded by a circle with radius 1 , such that the sum of the squares of the distances from to the endpoints of a given diameter is 3 . Then n is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: If and , a relation between and is:
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 30: Let be a point of hypotenuse (or its extension) of isosceles right triangle . Let . Then:
Answer Choices:
A. for a finite number of positions of
B. for an infinite number of positions of
C. only if is the midpoint of or an endpoint of
D. always
E. if is a trisection point of
Solution:
Problem 31: Let OABC be a unit square in the -plane with and . Let and be a transformation of the -plane into the uv-plane. The transform (or image) of the square is:
Answer Choices:
A.
.jpg)
.jpg)
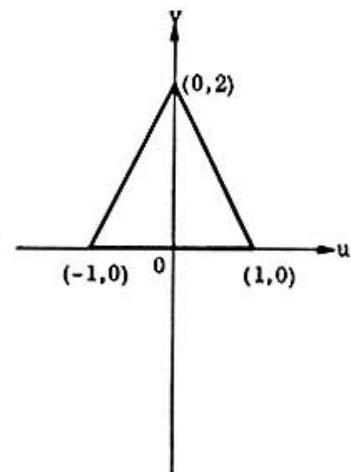
.jpg)
.jpg)
Solution:
Problem 32: Let a sequence be defined by the relation , , and . If is expressed as a polynomial in , the algebraic sum of its coefficients is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: Let and be the respective sums of the first terms of two arithmetic series. If for all n , the ratio of the eleventh term of the first series to the eleventh term of the second series, is:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: The remainder obtained by dividing by is a polynomial of degree less than 2 . Then may be written as:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: Let be the -coordinate of the left end point of the intersection of the graphs of and where . Let . Then, as is made arbitrarily close to zero, the value of is:
Answer Choices:
A. arbitrarily close to zero
B. arbitrarily close to
C. arbitrarily close to
D. arbitrarily large
E. undetermined
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions