¶ 1985 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1985 AHSME problems, please refer below:
Problem 1: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: In an arcade game, the "monster" is the shaded sector of a circle of radius cm, as shown in the figure. The missing piece (the mouth) has central angle . What is the perimeter of the monster in cm?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: In right with legs and , arcs of circles are drawn, one with center and radius , the other with center and radius . They intersect the hypotenuse in and . Then has length
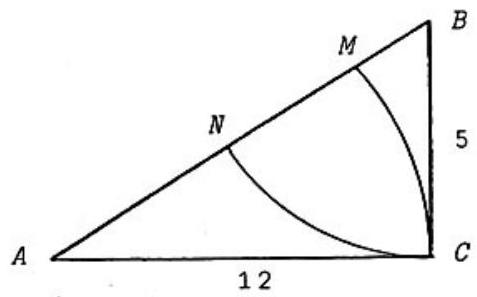
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A large bag of coins contains pennies, dimes and quarters. There are twice as many dimes as pennies and three times as many quarters as dimes. An amount of money which could be in the bag is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Which terms must be removed from the sum
if the sum of the remaining terms is to equal
Answer Choices:
A. and
B. and
C. and
D. and
E. and
Solution:
Problem 6: One student in a class of boys and girls is to be chosen to represent the class. Each student is equally likely to be chosen and the probability that a boy is chosen is of the probability that a girl is chosen. The ratio of the number of boys to the total number of boys and girls is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: In some computer languages (such as APL), when there are no parentheses in an algebraic expression, the operations are grouped from right to left. Thus, in such languages means the same as in ordinary algebraic notation. If is evaluated in such a language, the result in ordinary algebraic notation would be
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let be real numbers with and nonzero. The solution to is less than the solution to if and only if
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The odd positive integers, , , are arranged in five columns continuing with the pattern shown below. Counting from the left, the column in which appears is the
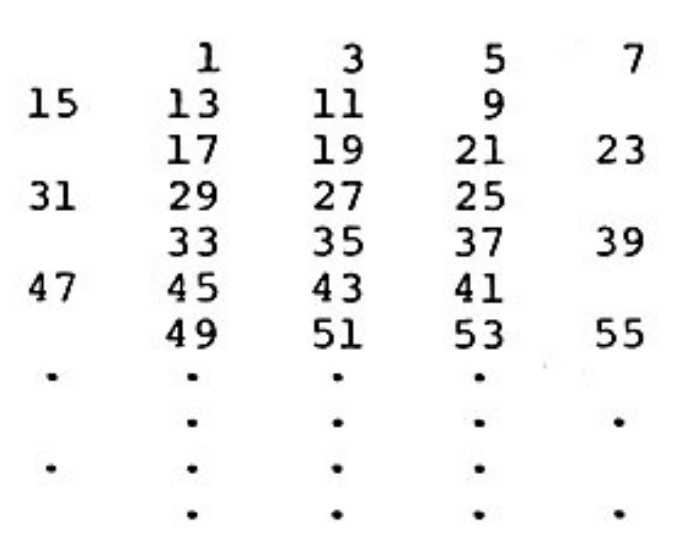
Answer Choices:
A. first
B. second
C. third
D. fourth
E. fifth
Solution:
Problem 10: An arbitrary circle can intersect the graph of in
Answer Choices:
A. at most points
B. at most points
C. at most points
D. at most points
E. more than points
Solution:
Problem 11: How many distinguishable rearrangements of the letters in have both the vowels first? (For instance, is one such arrangement, but is not.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let and be distinct prime numbers, where is not considered a prime. Which of the following is the smallest positive perfect cube having as a divisor?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Pegs are put in a board unit apart both horizontally and vertically. A rubber band is stretched over pegs as shown in the figure, forming a quadrilateral. Its area in square units is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If and are positive numbers such that and , then the value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If and , then the value of is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 17: Diagonal of rectangle is divided into three segments of length by parallel lines and that pass through and and are perpendicular to . The area of , rounded to one decimal place, is
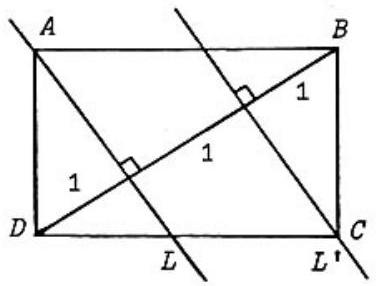
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Six bags of marbles contain , , , , and marbles, respectively. One bag contains chipped marbles only. The other bags contain no chipped marbles. Jane takes three of the bags and George takes two of the others. Only the bag of chipped marbles remains. If Jane gets twice as many marbles as George, how many chipped marbles are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Consider the graphs of and , where is a positive constant and and are real variables. In how many points do the two graphs intersect?
Answer Choices:
A. exactly
B. exactly
C. at least , but the number varies for different positive values of
D. for at least one positive value of
E. none of these
Solution:
Problem 20: A wooden cube with edge length units (where is an integer ) is painted black all over. By slices parallel to its faces, the cube is cut into smaller cubes each of unit edge length. If the number of smaller cubes with just one face painted black is equal to the number of smaller cubes completely free of paint, what is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 21: How many integers satisfy the equation
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 22: In a circle with center is a diameter, is a chord, and . Then the length of is
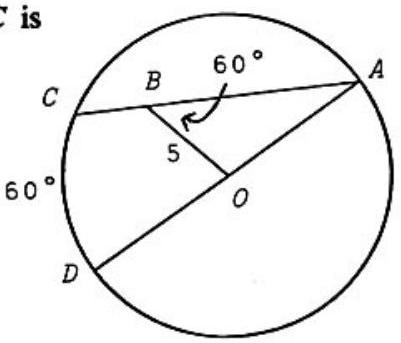
Answer Choices:
A.
B.
C.
D.
E. none of the above
Solution:
Problem 23: If and , where , then which of the following is not correct?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A non-zero digit is chosen in such a way that the probability of choosing digit is . The probability that the digit is chosen is exactly the probability that the digit chosen is in the set
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The volume of a certain rectangular solid is , its total surface area is , and its three dimensions are in geometric progression. The sum of the lengths in cm of all the edges of this solid is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Find the least positive integer for which is a non-zero reducible fraction.
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 27: Consider a sequence , defined by:
What is the smallest value of for which is an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: In , we have and . What is
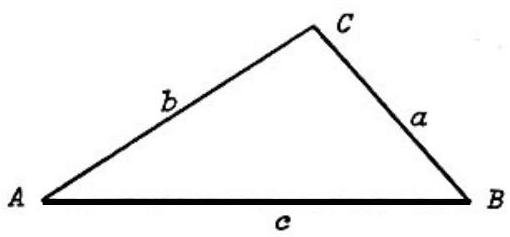
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 29: In their base representations, the integer consists of a sequence of eights and the integer consists of a sequence of fives. What is the sum of the digits of the base representation of the integer
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Let be the greatest integer less than or equal to . Then the number of real solutions to is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions