¶ 1986 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1986 AHSME problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If the line in the -plane has half the slope and twice the -intercept of the line , then an equation for is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: In the figure, has a right angle at and . If is the bisector of , then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let be the statement
"If the sum of the digits of the whole number is divisible by , then is divisible by ."
A value of which shows to be false is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 5: Simplify .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Using a table of a certain height, two identical blocks of wood are placed as shown in Figure . Length is found to be inches. After rearranging the blocks as in Figure , length is found to be inches. How high is the table?
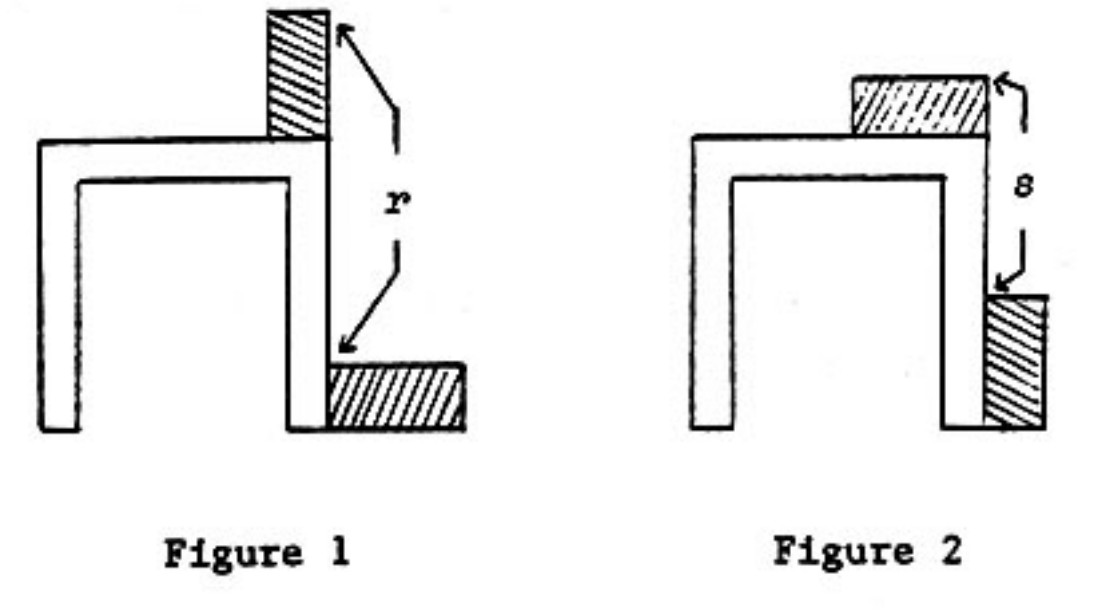
Answer Choices:
A. inches
B. inches
C. inches
D. inches
E. inches
Solution:
Problem 7: The sum of the greatest integer less than or equal to and the least integer greater than or equal to is . The solution set for is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The population of the United States in was . The area of the country is square miles. There are square feet in one square mile. Which number below best approximates the average number of square feet per person?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The product equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The permutations of are arranged in dictionary order, as if each were an ordinary five-letter word. The last letter of the word in this list is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: In , , and . Also, is the midpoint of side and is the foot of the altitude from to . The length of is
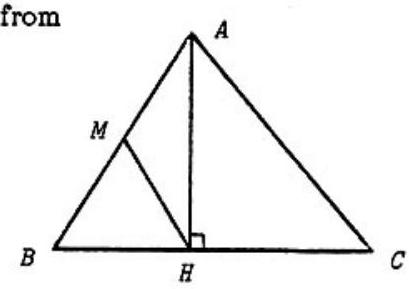
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: John scores on this year's . Had the old scoring system still been in effect, he would score only for the same answers. How many questions does he leave unanswered?
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 13: A parabola has vertex . If is on the parabola, then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Suppose hops, skips and jumps are specific units of length. If hops equals skips, jumps equals hops, and jumps equals meters, then one meter equals how many skips?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A student attempted to compute the average, , of , and by computing the average of and , and then computing the average of the result and . Whenever , the student's final result is
Answer Choices:
A. correct
B. always less than
C. always greater than
D. sometimes less than and sometimes equal to
E. sometimes greater than and sometimes equal to
Solution:
Problem 16: In and side is extended, as shown in the figure, to a point so that is similar to . The length of is
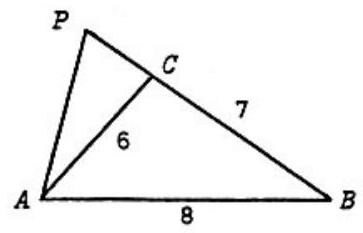
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A drawer in a darkened room contains red socks, green socks, blue socks and black socks. A youngster selects socks one at a time from the drawer but is unable to see the color of the socks drawn. What is the smallest number of socks that must be selected to guarantee that the selection contains at least pairs? (A pair of socks is two socks of the same color. No sock may be counted in more than one pair.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A plane intersects a right circular cylinder of radius forming an ellipse. If the major axis of the ellipse is longer than the minor axis, the length of the major axis is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A park is in the shape of a regular hexagon km on a side. Starting at a corner, Alice walks along the perimeter of the park for a distance of km. How many kilometers is she from her starting point?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Suppose and are inversely proportional and positive. If increases by , then decreases by
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: In the configuration below, is measured in radians, is the center of the circle, and are line segments, and is tangent to the circle at .
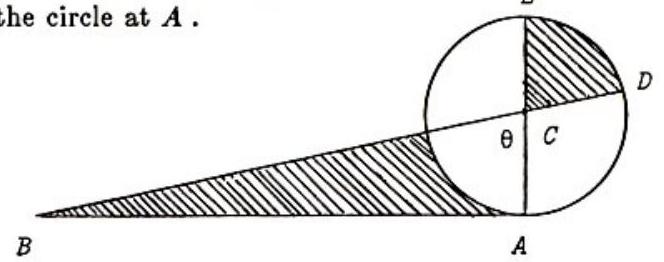
A necessary and sufficient condition for the equality of the two shaded areas, given , is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Six distinct integers are picked at random from . What is the probability that, among those selected, the second smallest is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 23: Let . How many positive integers are factors of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let , where and are integers. If is a factor of both and , what is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: If is the greatest integer less than or equal to , then
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 26: It is desired to construct a right triangle in the coordinate plane so that its legs are parallel to the and axes and so that the medians to the midpoints of the legs lie on the lines and . The number of different constants for which such a triangle exists is
Answer Choices:
A.
B.
C.
D.
E. more than 3
Solution:
Problem 27: In the adjoining figure, is a diameter of the circle, is a chord parallel to , and intersects at , with . The ratio of the area of to that of is
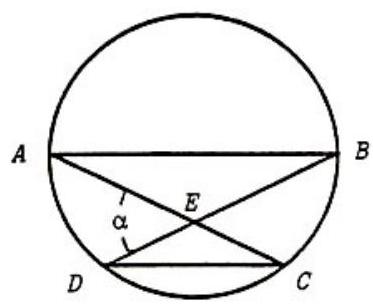
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: is a regular pentagon. dropped from onto extended and extended, respectively. Let be the center of the pentagon. If , then equals
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Two of the altitudes of the scalene triangle have length and . If the length of the third altitude is also an integer, what is the biggest it can be?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 30: The number of real solutions of the simultaneous equations
is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions