¶ 1987 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1987 AHSME problems, please refer below:
Problem 1: equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: As shown in the figure, a triangular corner with side lengths is cut from equilateral triangle of side length . The perimeter of the remaining quadrilateral is
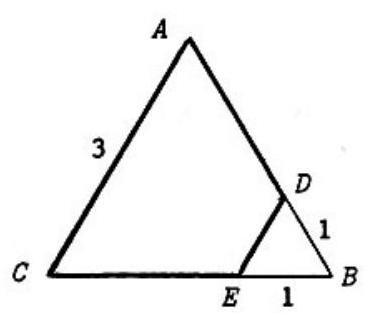
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: How many primes less than have as the ones digit? (Assume the usual base representation.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A student recorded the exact percentage frequency distribution for a set of measurements, as shown to the right. However, the student neglected to indicate , the total number of measurements. What is the smallest possible value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
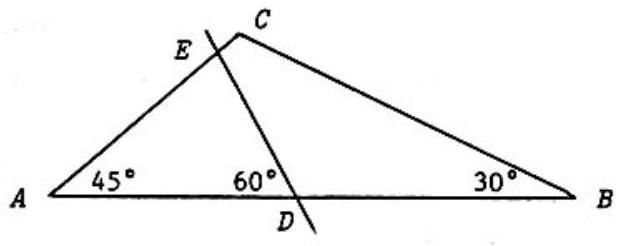
Problem 6: In the shown, is some interior point, and are the measures of angles in degrees. Solve for in terms of and .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If , which of the four quantities is the largest?
Answer Choices:
A.
B.
C.
D.
E. none of these answers
Solution:
Problem 8: In the figure the sum of the distances and is
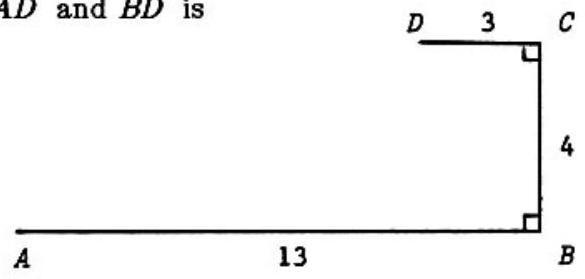
Answer Choices:
A. to
B.
C. to
D. to
E.
Solution:
Problem 9: The first four terms of an arithmetic sequence are . The ratio of to is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: How many ordered triples of non-zero real numbers have the property that each number is the product of the other two?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Let be a constant. The simultaneous equations
have a solution () inside Quadrant I if and only if
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: In an office, at various times during the day the boss gives the secretary a letter to type, each time putting the letter on top of the pile in the secretary's in-box. When there is time, the secretary takes the top letter off the pile and types it. If there are five letters in all, and the boss delivers them in the order , which of the following could not be the order in which the secretary types them?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A long piece of paper cm wide is made into a roll for cash registers by wrapping it times around a cardboard tube of diameter cm, forming a roll cm in diameter. Approximate the length of the paper in meters. (Pretend the paper forms concentric circles with diameters evenly spaced from cm to cm.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: is a square and and are the midpoints of and respectively. Then
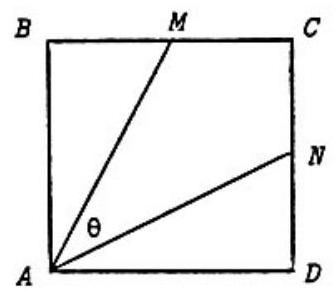
Answer Choices:
A.
B.
C.
D.
E. none of these answers
Solution:
Problem 15: If is a solution to the system
find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A cryptographer devises the following method for encoding positive integers. First, the integer is expressed in base . Second, a -to- correspondence is established between the digits that appear in the expressions in base and the elements of the set . Using this correspondence, the cryptographer finds that three consecutive integers in increasing order are coded as , respectively. What is the base- expression for the integer coded as
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In a mathematics competition, the sum of the scores of Bill and Dick equalled the sum of the scores of Ann and Carol. If the scores of Bill and Carol had been interchanged, then the sum of the scores of Ann and Carol would have exceeded the sum of the scores of the other two. Also, Dick's score exceeded the sum of the scores of Bill and Carol. Determine the order in which the four contestants finished, from highest to lowest. Assume all scores were nonnegative.
Answer Choices:
A. Dick, Ann, Carol, Bill
B. Dick, Ann, Bill, Carol
C. Dick, Carol, Bill, Ann
D. Ann, Dick, Carol, Bill
E. Ann, Dick, Bill, Carol
Solution:
Problem 18: It takes algebra books (all the same thickness) and geometry books (all the same thickness, which is greater than that of an algebra book) to completely fill a certain shelf. Also, of the algebra books and of the geometry books would fill the same shelf. Finally, of the algebra books alone would fill this shelf. Given that are distinct positive integers, it follows that is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Which of the following is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Evaluate
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 21: There are two natural ways to inscribe a square in a given isosceles right triangle. If it is done as in Figure below, then one finds that the area of the square is . What is the area (in ) of the square inscribed in the same as shown in Figure below?
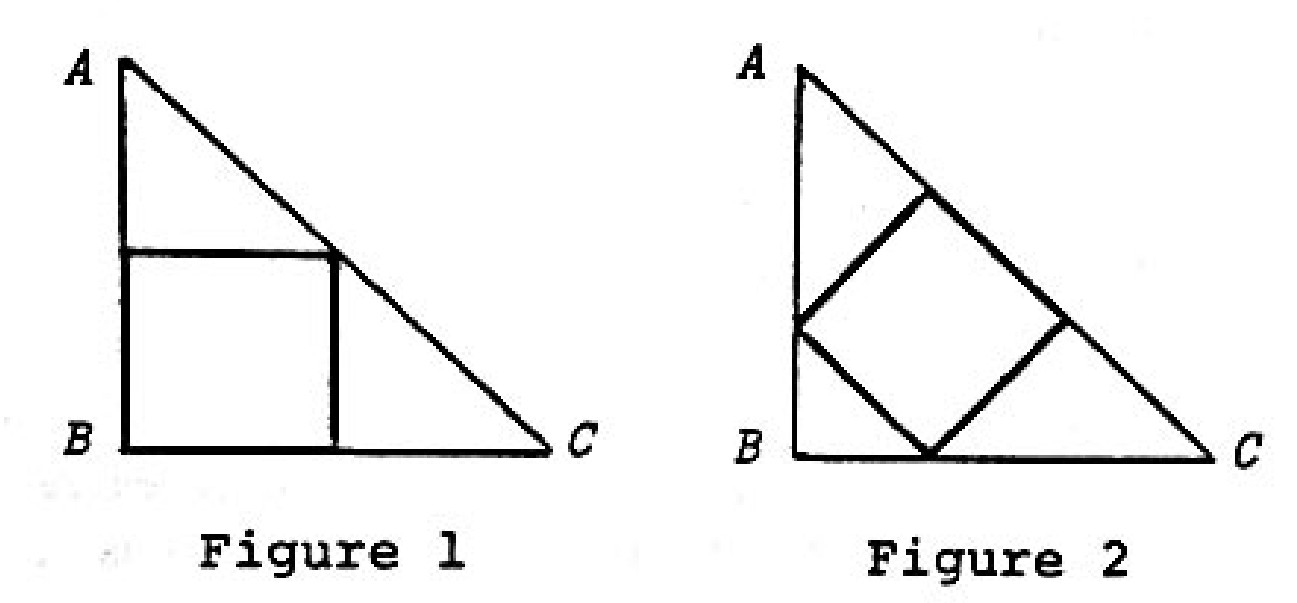
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A ball was floating in a lake when the lake froze. The ball was removed (without breaking the ice), leaving a hole cm across at the top and cm deep. What was the radius of the ball (in centimeters)?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: If is a prime and both roots of are integers, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: How many polynomial functions of degree satisfy
Answer Choices:
A.
B.
C.
D. finitely many but more than 2
E. infinitely many
Solution:
Problem 25: is a triangle: and both the coordinates of are integers. What is the minimum area can have?
Answer Choices:
A.
B.
C.
D.
E. there is no minimum
Solution:
Problem 26: The amount is split into two nonnegative real numbers uniformly at random, for instance, into and , or into and . Then each number is rounded to its nearest integer, for instance, and in the first case above, and in the second. What is the probability that the two integers sum to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: A cube of cheese is cut along the planes and . How many pieces are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Let be real numbers. Suppose that all the roots of are complex numbers lying on a circle in the complex plane centered at and having radius . The sum of the reciprocals of the roots is necessarily
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Consider the sequence of numbers defined recursively by and for by when is even and by when is odd. Given that , the sum of the digits of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: In the figure, has and . A line , with on and , divides into two pieces of equal area. (Note: the figure may not be accurate; perhaps is on instead of .) The ratio is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions