¶ 1988 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1988 AHSME problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Triangles and are similar, with corresponding to and to . If and , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Four rectangular paper strips of length and width are put flat on a table and overlap perpendicularly as shown. How much area of the table is covered?
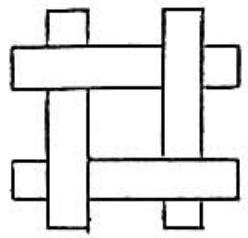
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The slope of the line is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If and are constants and
then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A figure is an equiangular parallelogram if and only if it is a
Answer Choices:
A. rectangle
B. regular polygon
C. rhombus
D. square
E. trapezoid
Solution:
Problem 7: Estimate the time it takes to send blocks of data over a communications channel if each block consists of "chunks" and the channel can transmit chunks per second.
Answer Choices:
A. seconds
B. seconds
C. seconds
D. minutes
E. hours
Solution:
Problem 8: If and , what is the ratio of to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: An table sits in the corner of a square room, as in Figure below. The owners desire to move the table to the position shown in Figure . The side of the room is feet. What is the smallest integer value of for which the table can be moved as desired without tilting it or taking it apart?
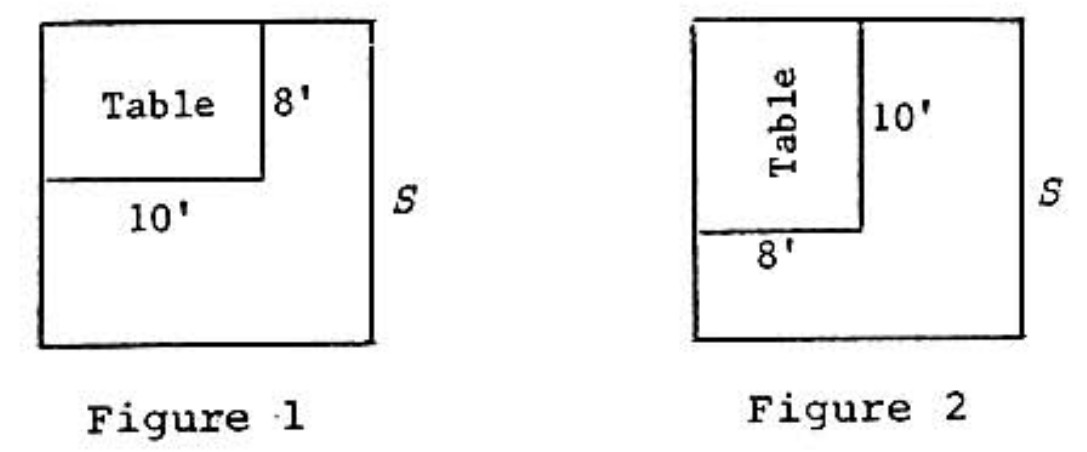
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In an experiment, a scientific constant is determined to be with an error of at most . The experimenter wishes to announce a value for in which every digit is significant. That is, whatever is, the announced value must be the correct result when is rounded to that number of digits. The most accurate value the experimenter can announce for is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: On each horizontal line in the figure below, the five large dots indicate the populations of cities and in the year indicated. Which city had the greatest percentage increase in population from to

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Each integer through is written on a separate slip of paper and all nine slips are put into a hat. Jack picks one of these slips at random and puts it back. Then Jill picks a slip at random. Which digit is most likely to be the units digit of the sum of Jack's integer and Jill's integer?
Answer Choices:
A.
B.
C.
D.
E. each digit is equally likely
Solution:
Problem 13: If then what is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: For any real number and positive integer , define
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If and are integers such that is a factor of , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: and are equilateral triangles with parallel sides and the same center, as in the figure. The distance between side and side is the altitude of . The ratio of the area of to the area of is
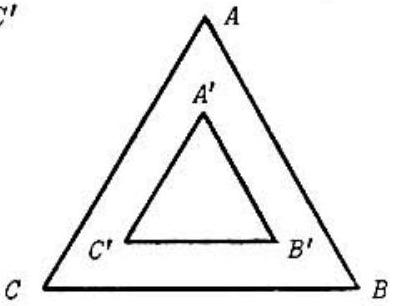
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If and , find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: At the end of a professional bowling tournament, the top bowlers have a playoff. First bowls . The loser receives prize and the winner bowls in another game. The loser of this game receives prize and the winner bowls . The loser of this game receives prize and the winner bowls . The winner of this game gets prize and the loser gets prize. In how many orders can bowlers through receive the prizes?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 19: Simplify
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In one of the adjoining figures a square of side is dissected into four pieces so that and are the midpoints of opposite sides and is perpendicular to . These four pieces can then be reassembled into a rectangle as shown in the second figure. The ratio of height to base, , in this rectangle is
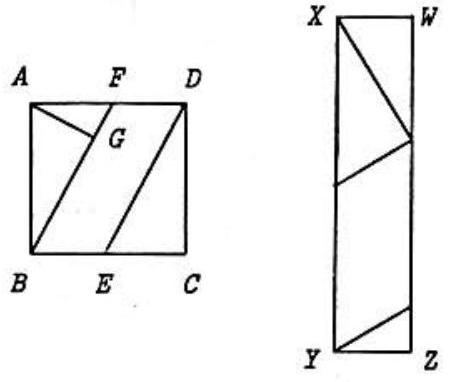
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The complex number satisfies . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: For how many integers does a triangle with side lengths , and have all its angles acute?
Answer Choices:
A.
B.
C.
D.
E. more than
Solution:
Problem 23: The six edges of tetrahedron measure , , , , and units. If the length of edge is , then the length of edge is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: An isosceles trapezoid is circumscribed around a circle. The longer base of the trapezoid is , and one of the base angles is . Find the area of the trapezoid.
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 25: , and are pairwise disjoint sets of people. The average ages of people in the sets and are given in the table below.
Find the average age of the people in the set .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Suppose that and are positive numbers for which
What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: In the figure, , and is tangent to the circle with center and diameter . In which one of the following cases is the area of an integer?
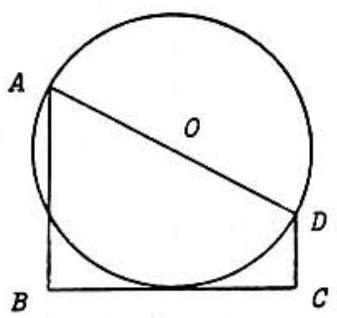
Answer Choices:
A. ,
B. ,
C. ,
D. ,
E. ,
Solution:
Problem 28: An unfair coin has probability of coming up heads on a single toss. Let be the probability that, in independent tosses of this coin, heads come up exactly times. If , then
Answer Choices:
A. must be
B. must be
C. must be greater than
D. is not uniquely determined
E. there is no value of for which
Solution:
Problem 29: You plot weight () against height () for three of your friends and obtain the points , , . If and , which of the following is necessarily the slope of the line which best fits the data? "Best fits" means that the sum of the squares of the vertical distances from the data points to the line is smaller than for any other line.
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 30: Let . Given , consider the sequence defined by for all . For how many real numbers will the sequence , , , take on only a finite number of different values?
Answer Choices:
A.
B. or
C. , , or
D. more than but finitely many
E. infinitely many
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions